题目内容
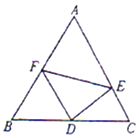
【题目】如图，在边长为2的正三角形△ABC中，D为BC的中点，E，F分别在边CA，AB上．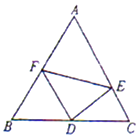 
（1）若 
，求CE的长；
（2）若∠EDF=60°，问：当∠CDE取何值时，△DEF的面积最小？并求出面积的最小值．
【答案】
（1）解：在△CDE中， 
，
由余弦定理得，DE2=CD2+CE2﹣2×CD×CE×cos60°，
得CE2﹣CE﹣1=0，解得 
；
（2）解：设∠CDE=α，300≤α≤900，
在△CDE中，由正弦定理，得 
，
所以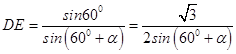 
，同理 
，
故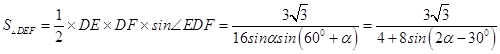 
，
因为300≤α≤900，300≤2α﹣300≤1500，
所以当α=600时，sin（2α﹣300）的最大值为1，此时△DEF的面积取到最小值．
即∠CDE=60°时，△DEF的面积的最小值为 
．
【解析】（1）在△CDE中，由已知及余弦定理可得CE2﹣CE﹣1=0，进而解得CE的值．（2）设∠CDE=α，300≤α≤900，在△CDE中，由正弦定理，可求DE= 
， 
，利用三角形面积公式可求S△DEF= 
，由范围300≤2α﹣300≤1500，利用正弦函数的图象和性质即可得解．
【考点精析】利用正弦定理的定义和余弦定理的定义对题目进行判断即可得到答案，需要熟知正弦定理:
；余弦定理:
;
;
．
练习册系列答案
相关题目
