题目内容
【题目】如图,点A与点A′在x轴上,且关于y轴对称,过点A′垂直于x轴的直线与抛物线y2=2x交于两点B,C,点D为线段AB 上的动点,点E在线段AC上,满足 ![]() .
.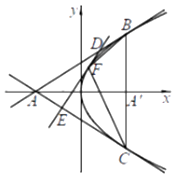
(1)求证:直线DE与此抛物线有且只有一个公共点;
(2)设直线DE与此抛物线的公共点F,记△BCF与△ADE的面积分别为S1、S2 , 求 ![]() 的值.
的值.
【答案】
(1)证明:设A(﹣2a2,0),A′(2a2,0),则B(2a2,2a),C(2a2,﹣2a),
设D(x1,y1), ![]() =λ
=λ ![]() ,
, ![]() =λ
=λ ![]() ,
,
∴(x1+2a2,y1)=λ(4a2,2a),故D的坐标((4λ﹣2)a2,2λa),
设E(x2,y2),由 ![]() =λ
=λ ![]() ,则(x2﹣2a2,y2+2a)=λ(﹣4a2,2a),
,则(x2﹣2a2,y2+2a)=λ(﹣4a2,2a),
∴E((2﹣4λ)a2,(2λ﹣2)a),
∴直线DE的斜率为kDE= ![]() =
= ![]() ,
,
直线DE的方程:y﹣2λa= ![]() [x﹣(2﹣4λ)a2],
[x﹣(2﹣4λ)a2],
整理得:(4λ﹣2)ay﹣2λa(4λ﹣2)a=x﹣(4λ﹣2)a2,即x=2a(2λ﹣1)y﹣2a2(2λ﹣1)2,①
代入抛物线方程,y2=2[2a(2λ﹣1)y﹣2a2(2λ﹣1)2],
整理得:y2﹣4a(2λ﹣1)y+4a2(2λ﹣1)2=0,②
此时方程②的两个根相等,y=2a(2λ﹣1),
代入①,整理得x=2a2(2λ﹣1)2,
∴直线DE与此抛物线有且仅有一个公共点F(2a2(2λ﹣1)2,2a(2λ﹣1));
(2)解:由S1= ![]() ×丨BC丨×h=
×丨BC丨×h= ![]() ×4a×(2a2﹣xF)=4a3(4λ﹣4λ2),
×4a×(2a2﹣xF)=4a3(4λ﹣4λ2),
设直线DE与x轴交于点G,令y=0,代入方程①,x=2a(2λ﹣1)y﹣2a2(2λ﹣1)2,解得:x=2a2(2λ﹣1)2,
故丨AG丨=2a2﹣2a2(2λ﹣1)2=2a2(4λ﹣4λ2),
S2=S△ADG+S△AEG= ![]() ×丨AG丨×丨yD﹣yE丨=a2(4λ﹣4λ2)丨2λa﹣(2λ﹣2)a丨=2a3(4λ﹣4λ2),
×丨AG丨×丨yD﹣yE丨=a2(4λ﹣4λ2)丨2λa﹣(2λ﹣2)a丨=2a3(4λ﹣4λ2),
∴ ![]() =2,
=2,
∴ ![]() 的值2.
的值2.
【解析】(1)设A及B,C点坐标,根据相似关系,设 ![]() =λ
=λ ![]() ,
, ![]() =λ
=λ ![]() ,根据向量的坐标运算,求得D及E点坐标,求得直线DE的方程,将直线方程代入抛物线方程,有且仅有一个解,则直线DE与此抛物线有且只有一个公共点;(2)根据三角形的面积公式,求得S1,令y=0,求得G点坐标及丨AG丨,则S2=S△ADG+S△AEG=
,根据向量的坐标运算,求得D及E点坐标,求得直线DE的方程,将直线方程代入抛物线方程,有且仅有一个解,则直线DE与此抛物线有且只有一个公共点;(2)根据三角形的面积公式,求得S1,令y=0,求得G点坐标及丨AG丨,则S2=S△ADG+S△AEG= ![]() ×丨AG丨×丨yD﹣yE丨=2a3(4λ﹣4λ2),即可求得
×丨AG丨×丨yD﹣yE丨=2a3(4λ﹣4λ2),即可求得 ![]() 的值.
的值.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案