题目内容
【题目】在平面直角坐标系xOy中,曲线C的参数方程为 ![]() (θ为参数).在极坐标系(与平面直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,直线l的方程为
(θ为参数).在极坐标系(与平面直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,直线l的方程为 ![]() .
.
(1)求曲线C的普通方程及直线l的直角坐标方程;
(2)设P是曲线C上的任意一点,求点P到直线l的距离的最大值.
【答案】
(1)解:因为曲线C的参数方程为 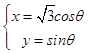 (θ为参数).
(θ为参数).
所以 ![]() ,
,
所以曲线C的普通方程为 ![]() ,
,
因为直线l的方程为 ![]() .
.
展开得ρsinθ﹣ρcosθ=3,即y﹣x=3,
所以直线l的直角坐标方程为x﹣y+3=0;
(2)解:设 ![]() ,
,
则点P到直线l的距离为 
等号成立当且仅当 ![]() ,
,
即 ![]() ,即
,即 ![]() 时成立,
时成立,
因此点P到直线l的距离的最大值为 ![]() .
.
【解析】(1)曲线C的参数方程消去参数θ,能求出曲线C的普通方程;直线l的极坐标方程转化为ρsinθ﹣ρcosθ=3,由此能求出直线l的直角坐标方程.(2)设 ![]() ,利用点到直线的距离公式求出点P到直线l的距离,由此能求出点P到直线l的距离的最大值.
,利用点到直线的距离公式求出点P到直线l的距离,由此能求出点P到直线l的距离的最大值.

练习册系列答案
相关题目
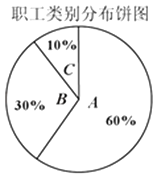
【题目】某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为A、B、C三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
工种类别 | A | B | C |
赔付频率 | | | |
(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.