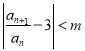题目内容
【题目】某射击运动员每次击中目标的概率是![]() ,在某次训练中,他只有4发子弹,并向某一目标射击.
,在某次训练中,他只有4发子弹,并向某一目标射击.
(1)若4发子弹全打光,求他击中目标次数![]() 的数学期望;
的数学期望;
(2)若他击中目标或子弹打光就停止射击,求消耗的子弹数![]() 的分布列.
的分布列.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】分析:(1)他击中目标次数![]() 可能取的值为0,1,2,3,4 ,由题意,随机变量
可能取的值为0,1,2,3,4 ,由题意,随机变量![]() 服从二项分布,即
服从二项分布,即![]() ~
~![]() ,则可求 4发子弹全打光,击中目标次数
,则可求 4发子弹全打光,击中目标次数![]() 的数学期望;
的数学期望;
(2)由题意随机变量![]() 可能取的值是1,2,3,4 ,由此可求他击中目标或子弹打光就停止射击,求消耗的子弹数
可能取的值是1,2,3,4 ,由此可求他击中目标或子弹打光就停止射击,求消耗的子弹数![]() 的分布列
的分布列
详解:
(1)他击中目标次数![]() 可能取的值为0,1,2,3,4
可能取的值为0,1,2,3,4
由题意,随机变量![]() 服从二项分布,即
服从二项分布,即![]() ~
~![]()
![]()
(若列出分布列表格计算期望,酌情给分)
(2)由题意随机变量![]() 可能取的值是1,2,3,4
可能取的值是1,2,3,4
![]()
![]()
![]()
![]()
| 1 | 2 | 3 | 4 |
| 0.9 | 0.09 | 0.009 | 0.001 |

练习册系列答案
相关题目
【题目】随着人们生活水平的不断提高,家庭理财越来越引起人们的重视.某一调查机构随机调查了5个家庭的月收入与月理财支出(单位:元)的情况,如下表所示:
月收入 | 8 | 10 | 9 | 7 | 11 |
月理财支出 |
|
|
|
|
|
(I)在下面的坐标系中画出这5组数据的散点图;
(II)根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(III)根据(II)的结果,预测当一个家庭的月收入为![]() 元时,月理财支出大约是多少元?
元时,月理财支出大约是多少元?
(附:回归直线方程![]() 中,
中, ,
,![]() .)
.)