题目内容
【题目】已知函数f(x)=(2﹣a)(x﹣1)﹣2lnx,(a∈R). (Ⅰ)当a=1时,求f(x)的单调区间;
(Ⅱ)若函数f(x)在(0, ![]() )上无零点,求a的取值范围.
)上无零点,求a的取值范围.
【答案】解:(Ⅰ)当a=1时,f(x)=x﹣1﹣2lnx,则f′(x)=1﹣ ![]() , 由f′(x)>0,得x>2,由f′(x)<0,得0<x<2,
, 由f′(x)>0,得x>2,由f′(x)<0,得0<x<2,
故f(x)的单调减区间为(0,2],单调增区间为[2,+∞);
(Ⅱ)因为f(x)<0在区间(0, ![]() )上恒成立不可能,
)上恒成立不可能,
故要使函数f(x)在(0, ![]() )上无零点,
)上无零点,
只要对任意的x∈(0, ![]() ),f(x)>0恒成立,
),f(x)>0恒成立,
即对x∈(0, ![]() ),a>2﹣
),a>2﹣ ![]() 恒成立.
恒成立.
令h(x)=2﹣ ![]() ,x∈(0,
,x∈(0, ![]() ),
),
则h′(x)= 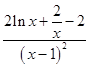 ,
,
再令m(x)=2lnx+ ![]() ﹣2,x∈(0,
﹣2,x∈(0, ![]() ),
),
则m′(x)= ![]() <0,
<0,
故m(x)在(0, ![]() )上为减函数,
)上为减函数,
于是,m(x)>m( ![]() )=4﹣3ln3>0,
)=4﹣3ln3>0,
从而h(x)>0,于是h(x)在(0, ![]() )上为增函数,
)上为增函数,
所以h(x)<h( ![]() )=2﹣3ln3,
)=2﹣3ln3,
∴a的取值范围为[2﹣3ln3,+∞)
【解析】(Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;(Ⅱ)问题转化为x∈(0, ![]() ),a>2﹣
),a>2﹣ ![]() 恒成立,令h(x)=2﹣
恒成立,令h(x)=2﹣ ![]() ,x∈(0,
,x∈(0, ![]() ),根据函数的单调性求出h(x)的最大值,从而求出a的范围即可.
),根据函数的单调性求出h(x)的最大值,从而求出a的范围即可.
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.

【题目】如图,在平面直角坐标系xOy中,已知椭圆 ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,焦点到相应准线的距离为1.
,焦点到相应准线的距离为1. 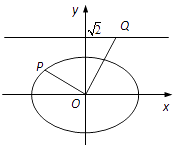
(1)求椭圆的标准方程;
(2)若P为椭圆上的一点,过点O作OP的垂线交直线 ![]() 于点Q,求
于点Q,求 ![]() 的值.
的值.
【题目】从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:
分组(重量) |
|
|
|
|
频数(个) | 5 | 10 | 20 | 15 |
(1) 根据频数分布表计算苹果的重量在![]() 的频率;
的频率;
(2) 用分层抽样的方法从重量在![]() 和
和![]() 的苹果中共抽取4个,其中重量在
的苹果中共抽取4个,其中重量在![]() 的有几个?
的有几个?
(3) 在(2)中抽出的4个苹果中,任取2个,求重量在![]() 和
和![]() 中各有1个的概率.
中各有1个的概率.