题目内容
【题目】如图，在矩形
中，
，
，
是
的中点.将
沿
折起，使折起后平面
平面
，则异面直线和所成角的余弦值为（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
由题意，取AB中点F，连接CF，则CF∥AE，可得直线AE和CD所成角的平面角为∠DCF，结合已知求解△DCF三边长度，满足直角三角形，可得cos∠DCF.
由题意，
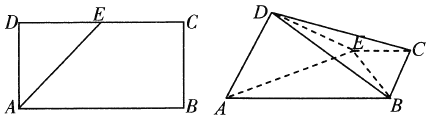
取AB中点F，连接CF，则CF∥AE，可得直线AE和CD所成角的平面角为∠DCF，（如图）
过D作DM垂直AE于M，平面DAE⊥平面ABCE，
AD＝DE，
∴DM⊥AE，
∴DM⊥平面ABCE，∴DM⊥MF，
且AM＝DM
，结合平面图形可得：FM=
, ∴DF=
=1,CF=
,
又
=
, ∴
=
3,
∴在△DFC中，=
,
∴△DFC是直角三角形且DF⊥FC，
可得cos∠DCF
．
故选A.
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量
(吨)与相应的生产能耗
(吨)标准煤的几组对照数据
|
|
|
|
|
|
|
|
|
|
(1)请根据上表提供的数据，用最小二乘法求出关于的线性回归方程
；
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(1)求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式：
【题目】某地区为了调查高粱的高度、粒的颜色与产量的关系,对700棵高粱进行抽样调查,得到高度频数分布表如下:
表1：红粒高粱频数分布表
农作物高度( |
|
|
|
|
|
|
频 数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2：白粒高粱频数分布表
农作物高度( |
|
|
|
|
|
|
频 数 | 1 | 7 | 12 | 6 | 3 | 1 |
(1)估计这700棵高粱中红粒高粱的棵数;
(2)估计这700棵高粱中高粱高(
)在
的概率；
(3)在样本的红粒高粱中，从高度(单位：)在
中任选3棵，设
表示所选3棵中高(单位：)在
的棵数，求的分布列和数学期望
．
