题目内容
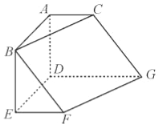
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() ,
,![]() .
.

(1)证明:平面![]() 平面
平面![]() .
.
(2)若![]() ,试问:
,试问:![]() 是否与平面
是否与平面![]() 平行?若平行,求三棱锥
平行?若平行,求三棱锥![]() 的体积;若不平行,请说明理由.
的体积;若不平行,请说明理由.
【答案】(1)详见解析;(2)两者平行,且![]()
![]() .
.
【解析】
(1)利用![]() 平面
平面![]() ,证得
,证得![]() 平面
平面![]() ,得到
,得到![]() ,利用余弦定理证得
,利用余弦定理证得![]() ,由此证得
,由此证得![]() 平面
平面![]() ,从而证得平面
,从而证得平面![]() 平面
平面![]() .(2)取
.(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,通过证明四边形
,通过证明四边形![]() 为平行四边形,证得
为平行四边形,证得![]() ,同理证得
,同理证得![]() ,所以平面
,所以平面![]() 平面
平面![]() ,由此证得
,由此证得![]() 平面
平面![]() .利用
.利用![]() 求得三棱锥的体积.
求得三棱锥的体积.
(1)证明:因为AA1⊥平面ABC,
所以BB1⊥平面ABC,
因为![]() ,
,
所以AD⊥BB1.
在△ABD中,由余弦定理可得,![]() ,
,
则![]() ,
,
所以AD⊥BC,
又![]() ,
,
所以AD⊥平面BB1C1C,
因为![]() ,
,
所以平面ADB1⊥平面BB1C1C.
(2)解:A1C与平面ADB1平行.
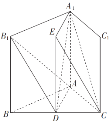
证明如下:取B1C1的中点E,连接DE,CE,A1E,
因为BD=CD,所以DE∥AA1,且DE=AA1,
所以四边形ADEA1为平行四边形,
则A1E∥AD.
同理可证CE∥B1D.
因为![]() ,
,
所以平面ADB1∥平面A1CE,
又![]() ,
,
所以A1C∥平面ADB1.
因为AA1∥BB1,
所以![]() ,
,
又![]() ,且易证BD⊥平面AA1D,
,且易证BD⊥平面AA1D,
所以![]() .
.

练习册系列答案
相关题目