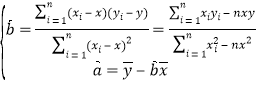题目内容
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,
轴正半轴为极轴建立极坐标系,![]() 点的极坐标为
点的极坐标为![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 经过点
经过点![]() .
.
(I)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的参数方程;
的参数方程;
(II)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求线段
两点,求线段![]() 的长.
的长.
【答案】(Ⅰ)曲线C的普通方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为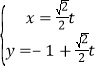 (
(![]() 为参数).(Ⅱ)
为参数).(Ⅱ)![]()
【解析】
(Ⅰ)根据sin2θ+cos2θ=1消去曲线C的参数θ可得普通方程;根据直线过的定点及斜率写出直线的参数方程;
(Ⅱ)将直线的参数方程与曲线![]() 的普通方程联立,得到关于t的一元二次方程,结合参数t的意义得到
的普通方程联立,得到关于t的一元二次方程,结合参数t的意义得到![]() ,利用根与系数的关系可得结果.
,利用根与系数的关系可得结果.
(Ⅰ)曲线C的参数方程为![]() (θ为参数),普通方程为
(θ为参数),普通方程为![]()
直线![]() 经过点
经过点![]() ,斜率为
,斜率为![]() ,直线
,直线![]() 的参数方程为
的参数方程为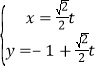 (
(![]() 为参数).
为参数).
(Ⅱ)将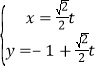 (
(![]() 为参数)代入
为参数)代入![]() ,化简整理得:
,化简整理得:![]() ,
,
设![]() 是方程的两根,则
是方程的两根,则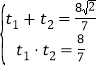 ,则
,则![]() .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
【题目】某种设备随着使用年限的增加,每年的维护费相应增加.现对一批该设备进行调查,得到这批设备自购入使用之日起,前5年平均每台设备每年的维护费用大致如表:
年份 |
|
|
|
|
|
维护费 |
|
|
|
|
|
已知![]() .
.
(I)求表格中![]() 的值;
的值;
(II)从这![]() 年中随机抽取两年,求平均每台设备每年的维护费用至少有
年中随机抽取两年,求平均每台设备每年的维护费用至少有![]() 年多于
年多于![]() 万元的概率;
万元的概率;
(Ⅲ)求![]() 关于
关于![]() 的线性回归方程;并据此预测第几年开始平均每台设备每年的维护费用超过
的线性回归方程;并据此预测第几年开始平均每台设备每年的维护费用超过![]() 万元.
万元.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式: