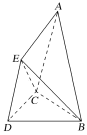
题目内容
【题目】已知实数
满足：有且仅有一个正方形，其四个顶点均在曲线
上.试求这个正方形的面积.
【答案】
【解析】
由于曲线
关于原点对称，所以该正方形的中心必过原点（否则，将这个正方形关于原点作对称又得到一个顶点均在曲线上的正方形）.
设正方形的一个顶点为
，则
、
、
是其他三个顶点.令
的斜率分别为
，则由
，得
， （1）
并且（由于
在曲线上）有
， （2）
（3）
由（2）、（3）得
. （4）
结合（1）得
（5）
这说明方程
（6）
有解
.并且对（6）的任一解
，结合（1）可求出（均为实数，因为）.再由（2）定出
，它们满足（3）的第一个等式，由（5）有
.
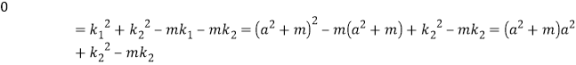
从而，（3）的第二个等式也成立.
确定的四点
构成曲线上的正方形.
因为已知曲线上只有一个正方形，所以方程（6）只有两个相同的解.
由
，得
.
由（2）、（3）得
.
故
.从而
.
则正方形的边长
.
即正方形的面积
.
【题目】企业需为员工缴纳社会保险，缴费标准是根据职工本人上一年度月平均工资（单位：元）的
缴纳，
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
t | 1 | 2 | 3 | 4 | 5 |
y | 270 | 330 | 390 | 460 | 550 |
某企业员工甲在2014年至2018年各年中每月所撒纳的养老保险数额y（单位：元）与年份序号t的统计如下表：
（1）求出t关于t的线性回归方程
；
（2）试预测2019年该员工的月平均工资为多少元？
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
（注：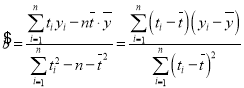
，
，其中
）
【题目】下面给出三个游戏，袋子中分别装有若干只有颜色不同的小球（大小，形状，质量等均一样），从袋中无放回地取球，则其中不公平的游戏是______.
游戏1 | 游戏2 | 游戏3 | |
球数 | 3个黑球和一个白球 | 一个黑球和一个白球 | 2个黑球和2个白球 |
取法 | 取1个球，再取1个球 | 取1个球 | 取1个球，再取1个球 |
胜利 规则 | 取出的两个球同色→甲胜 | 取出的球是黑球→甲胜 | 取出的两个球同色→甲胜 |
取出的两个球不同色→乙胜 | 取出的球是白球→乙胜 | 取出的两个球不同色→乙胜 |
