题目内容
【题目】已知空间几何体ABCDE中，△BCD与△CDE均是边长为2的等边三角形，△ABC是腰长为3的等腰三角形，平面CDE⊥平面BCD，平面ABC⊥平面BCD.
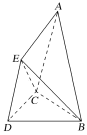
(1)试在平面BCD内作一条直线，使得直线上任意一点F与E的连线EF均与平面ABC平行，并给出证明；
(2)求三棱锥E－ABC的体积.
【答案】（1）取DC的中点N，取BD的中点M，连接MN，则MN即为所求，证明见解析（2）
【解析】
（1）取DC的中点N，取BD的中点M，连接MN，则MN即为所求，证明EN∥AH，MN∥BC可得平面EMN∥平面ABC即可（2）因为点E到平面ABC的距离与点N到平面ABC的距离相等，求三棱锥E－ABC的体积可转化为求三棱锥N－ABC的体积，根据体积公式计算即可.
(1)如图所示，取DC的中点N，取BD的中点M，连接MN，则MN即为所求.
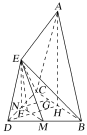
证明：连接EM，EN，取BC的中点H，连接AH，
∵△ABC是腰长为3的等腰三角形，H为BC的中点，
∴AH⊥BC，又平面ABC⊥平面BCD，平面ABC∩平面BCD＝BC，AH平面ABC，
∴AH⊥平面BCD，同理可证EN⊥平面BCD，
∴EN∥AH，
∵EN平面ABC，AH平面ABC，
∴EN∥平面ABC.
又M，N分别为BD，DC的中点，
∴MN∥BC，
∵MN平面ABC，BC平面ABC，
∴MN∥平面ABC.
又MN∩EN＝N，MN平面EMN，EN平面EMN，
∴平面EMN∥平面ABC，
又EF平面EMN，
∴EF∥平面ABC，
即直线MN上任意一点F与E的连线EF均与平面ABC平行.
(2)连接DH，取CH的中点G，连接NG，则NG∥DH，
由(1)可知EN∥平面ABC，
∴点E到平面ABC的距离与点N到平面ABC的距离相等，
又△BCD是边长为2的等边三角形，
∴DH⊥BC，
又平面ABC⊥平面BCD，平面ABC∩平面BCD＝BC，DH平面BCD，
∴DH⊥平面ABC，∴NG⊥平面ABC，
易知DH＝
，∴NG＝
，
又S△ABC＝
·BC·AH＝×2×
＝2
，
∴VE－ABC＝
·S△ABC·NG＝.
【题目】某超市为了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100名顾客的相关数据，如下表所示：
已知这100位顾客中一次性购物超过8件的顾客占55%.
一次性购物 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
顾客数（人） |
| 30 | 25 |
| 10 |
结算时间（分/人） | 1 | 1.5 | 2 | 2.5 | 3 |
（1）求
，
的值；
（2）求一位顾客一次购物的结算时间超过2分钟的概率（频率代替概率）.
【题目】某企业生产某种产品，为了提高生产效益，通过引进先进的生产技术和管理方式进行改革，并对改革后该产品的产量x（万件）与原材料消耗量y（吨）及100件产品中合格品与不合格品数量作了记录，以便和改革前作对照分析，以下是记录的数据：
表一：改革后产品的产量和相应的原材料消耗量
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
表二：改革前后定期抽查产品的合格数与不合格数
合格品的数量 | 不合格品的数量 | 合计 | |
改革前 | 90 | 10 | 100 |
改革后 | 85 | 15 | 100 |
合计 | 175 | 25 | 200 |
（1）请根据表一提供数据，用最小二乘法求出y关于x的线性回归方程
.
（2）已知改革前生产7万件产品需要6.5吨原材料，根据回归方程预测生产7万件产品能够节省多少原材料？
（3）请根据表二提供的数据，判断是否有90%的把握认为“改革前后生产的产品的合格率有差异”？
