题目内容
2.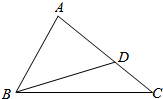 如图,△ABC中,∠B满足$\sqrt{2}$sinB-cosB=1,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$.
如图,△ABC中,∠B满足$\sqrt{2}$sinB-cosB=1,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$.(1)求tanB的值;
(2)求BC的长.
分析 (1)由$\sqrt{2}$sinB-cosB=1,可得3cos2B+2cosB-1=0,求出cosB,即可求tanB的值;
(2)利用余弦定理,建立方程组,即可求BC的长.
解答 解:(1)∵$\sqrt{2}$sinB-cosB=1,
∴$\sqrt{2}$sinB=cosB+1,
∴2sin2B=(cosB+1)2,
∴3cos2B+2cosB-1=0,
∵0°<B<180°,
∴cosB=$\frac{1}{3}$,
∴sinB=$\frac{2\sqrt{2}}{3}$,
∴tanB=2$\sqrt{2}$;
(2)设CD=x,BC=y,则AD=2x,
△ABD中,22=($\frac{4\sqrt{3}}{3}$)2+4x2-2•$\frac{4\sqrt{3}}{3}$•2x•cos∠ADB,
△CBD中,y2=($\frac{4\sqrt{3}}{3}$)2+x2-2•$\frac{4\sqrt{3}}{3}$•x•cos∠CDB,
相加可得4+y2=$\frac{32}{3}$+5x2,①
△ABC中,9x2=4+y2-2•2•y•$\frac{1}{3}$,②
①②联立可得y=$\frac{5\sqrt{29}-5}{6}$,
∴BC=$\frac{5\sqrt{29}-5}{6}$.
点评 本题考查同角三角函数关系,考查余弦定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
12.若极坐标方程ρ=ρ(θ)满足ρ(θ)=ρ(π-θ),则方程ρ=ρ(θ)表示的图形关于( )
| A. | 极轴对称 | B. | 极点对称 | C. | 射线θ=$\frac{π}{2}$对称 | D. | 不能确定 |