题目内容
10.若{1,2}⊆A⊆{1,2,3,4,5,6}则满足条件的集合A的个数是16.分析 根据题意A中必须有1,2这两个元素,因此A的个数应为集合{3,4,5,6}的子集的个数.
解答 解:∵{1,2}⊆A⊆{1,2,3,4,5},∴集合A中必须含有1,2两个元素,可以含有3,4,5,6.
因此满足条件的集合A为{1,2},{1,2,3},{1,2,4},{1,2,5},{1,2,6},{1,2,3,4},{1,2,3,5},{1,2,3,6},{1,2,4,5},{1,2,4,6},{1,2,5,6},{1,2,3,4,5},{1,2,3,4,6},{1,2,3,5,6},{1,2,4,5,6},{1,2,3,4,5,6}共16个.
故答案为:16.
点评 本题考查了子集的概念,熟练掌握由集合间的关系得到元素关系是解题的关键.有n个元素的集合其子集共有2n个.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
18.函数y=$\frac{\sqrt{1-x}}{2{x}^{2}-3x-2}$的定义域是( )
| A. | (-∞,1] | B. | (-∞,2] | C. | (-∞,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,2) | D. | (-∞,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1] |
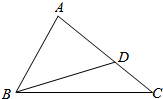 如图,△ABC中,∠B满足$\sqrt{2}$sinB-cosB=1,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$.
如图,△ABC中,∠B满足$\sqrt{2}$sinB-cosB=1,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$.