题目内容

11．某射手每次射击击中目标的概率是$\frac{4}{5}$，求这名射手在10次射击中，
（1）恰有8次击中目标的概率；
（2）至少有8次击中目标的概率．

分析 （1）由条件利用n次独立重复实验中恰好发生k次的概率计算公式，求得恰有8次击中目标的概率．
（2）由条件利用n次独立重复实验中恰好发生k次的概率计算公式，求得恰有8次击中目标的概率、恰有9次击中目标的概率、恰有10次击中目标的概率，再把这3个概率相加，即得所求．

解答 解：（1）∵某射手每次射击击中目标的概率是$\frac{4}{5}$，则这名射手在10次射击中恰有8次击中目标的概率为${C}_{10}^{8}$•${（\frac{4}{5}）}^{8}$•${（\frac{1}{5}）}^{2}$．
（2）至少有8次击中目标的概率为${C}_{10}^{8}$•${（\frac{4}{5}）}^{8}$•${（\frac{1}{5}）}^{2}$+${C}_{10}^{9}$•${（\frac{4}{5}）}^{9}$•$\frac{1}{5}$+${（\frac{4}{5}）}^{10}$．

点评 本题主要考查n次独立重复实验中恰好发生k次的概率，体现了转化、分类讨论的数学思想，属于基础题．

练习册系列答案
相关题目
1．从装有编号为1，2，3，…，n+1的n+1个球的口袋中取出m个球（0＜m≤n，m，n∈N），共有Cn+1m种取法．在这Cn+1m种取法中，不取1号球有C10Cnm种取法；必取1号球有C11Cnm-1种取法．所以C10Cnm+C11Cnm-1=Cn+1m，即Cnm+Cnm-1=Cn+1m成立．试根据上述思想，则有当1≤k≤m≤n，k，m，n∈N时，Cnm+Ck1Cnm-1+Ck2Cnm-2+…+CkkCnm-k=$C_{n+k}^m$．
2．复数i2015（i为虚数单位）的共轭复数是（　　）
A．1B．-1C．iD．-i
19．设函数f（x）是定义在R上的奇函数，且对任意x∈R都有f（x）=f（x+4），当x∈（0，2）时，f（x）=2x，则f（2015）+f（2012）的值为（　　）
A．-2B．-1C．$\frac{1}{2}$D．$\frac{3}{2}$
6．已知点（1，-2）和$（{\frac{{\sqrt{3}}}{3}，0}）$在直线l：ax-y-1=0（a≠0）的两侧，则直线l倾斜角的取值范围是（　　）
A．$（{\frac{π}{4}，\frac{π}{3}}）$B．$（{\frac{2π}{3}，\frac{5π}{6}}）$C．$（{0，\frac{π}{3}}）∪（{\frac{3π}{4}，π}）$D．$（{\frac{π}{3}，\frac{2π}{3}}）$
16．如图，正四棱柱ABCD-A1B1C1D1中，AA1=2AB．
（1）点P为棱CC1上一动点，求证：AP⊥B1D1；
（2）求AD1与平面A1CD所成角的正弦值．
3．在等比数列{an}中，若a3=4，a7=16，a5的值为（　　）
A．±8B．4C．8D．64
20．在平面直角坐标系xOy中，已知圆O1，圆O2均与x轴相切，且圆O1，O2都在射线y=mx（m＞0，x＞0）上．
（1）若O1的坐标为（3，1），过直线x-y+2=0上的一点P作圆O1的切线，切点分别为A，B两点，求PA长度的最小值；
（2）若圆O1，圆O2的半径之积为2，Q（2，2）是两圆的一个公共点，求两圆的另一条公切线的方程．
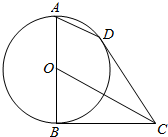1．如图所示，AB为圆O的直径，BC，CD为圆O的切线，B，D为切点．
（Ⅰ）求证：AB∥OC；
（Ⅱ）若圆O的半径为2，求AD•OC的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网