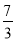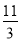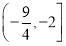题目内容
已知正项等比数列{an}满足:a3=a2+2a1,若存在两项am,an使得  =4a1,则
=4a1,则 的最小值为 ( ).
的最小值为 ( ).
A. B.
B. C.
C. D.不存在
D.不存在
A
【解析】设等比数列{an}的公比为q(q>0),
∵a3=a2+2a1,
∴a1q2=a1q+2a1,解之得q=2.
又 =4a1,
=4a1,
∴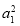 qm+n-2=16
qm+n-2=16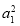 ,
,
∴2m+n-2=16.
因此m+n=6.
则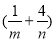 (m+n)=5+
(m+n)=5+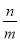 +
+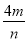 ≥9.
≥9.
当且仅当n=2m(即n=4,m=2)时取等号.
∴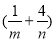 (m+n)的最小值为9,
(m+n)的最小值为9,
从而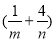 的最小值为
的最小值为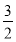 .
.

练习册系列答案
相关题目