题目内容
17.在△ABC中,若tan A•tan B<1,则△ABC的形状是( )| A. | 锐角三角形 | |
| B. | 直角三角形 | |
| C. | 钝角三角形 | |
| D. | 可能是锐角三角形,也可能是钝角三角形 |
分析 将已知条件tanA•tanB<1中的切化弦,逆用两角和的余弦判断即可.
解答 解:∵tanA•tanB<1,
∴1-$\frac{sinAsinB}{cosAcosB}$>0,即$\frac{cosAcosB-sinAsinB}{cosAcosB}$=$\frac{cos(A+B)}{cosAcosB}$=-$\frac{cosC}{cosAcosB}$>0,
∴$\frac{cosC}{cosAcosB}$<0.
∴A、B、C中必有一角为钝角,
∴这个三角形是钝角三角形.
故选:C.
点评 本题考查三角形的形状判断,考查转化与分析、运算能力,属于中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
12.若M点的极坐标为$({2,\frac{5π}{6}})$,则M点的直角坐标是( )
| A. | (-$\sqrt{3}$,1) | B. | (-$\sqrt{3}$,-1) | C. | ($\sqrt{3}$,-1) | D. | ($\sqrt{3}$,1) |
2.函数f(x)=$\sqrt{3}$x+2cosx在区间[0,$\frac{π}{2}$]上的最大值是( )
| A. | 2 | B. | $\frac{\sqrt{3}π}{2}$ | C. | $\frac{\sqrt{3}π+3}{3}$ | D. | 1 |
9.如图程序图输出的结果是( )
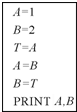
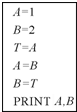
| A. | 2,1 | B. | 2,2 | C. | 1,2 | D. | 1,1 |
6.下列函数中,在其定义域内既是奇函数又是减函数的是( )
| A. | y=($\frac{1}{2}$)x,x∈R | B. | y=$\frac{1}{x-1}$,x≠1 | C. | y=x+sinx,x∈R | D. | y=-x3-x,x∈R |
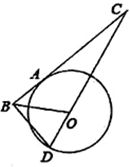 已知如图,A、D是⊙O上的点,A、B、C三点在一条直线上,直线CD经过圆心O,BD⊥BC,$\frac{BA}{AC}$=$\frac{DB}{DC}$.
已知如图,A、D是⊙O上的点,A、B、C三点在一条直线上,直线CD经过圆心O,BD⊥BC,$\frac{BA}{AC}$=$\frac{DB}{DC}$. 如图所示,已知半圆的直径AB=6cm,CD是半圆上长为2cm的弦,问:当弦CD在半圆上滑动时,AC和BD延长线的夹角是定值吗?若是,试求出这个定角的正弦值;若不是,请说明理由.
如图所示,已知半圆的直径AB=6cm,CD是半圆上长为2cm的弦,问:当弦CD在半圆上滑动时,AC和BD延长线的夹角是定值吗?若是,试求出这个定角的正弦值;若不是,请说明理由.