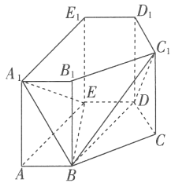
题目内容
【题目】设![]() 为等差数列
为等差数列![]() 的前n项和,
的前n项和,![]() 是正项等比数列,且
是正项等比数列,且![]() ,
,![]() .在①
.在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,回答下列为题:
这三个条件中任选一个,回答下列为题:
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)如果![]() (m,
(m,![]() ),写出m,n的关系式
),写出m,n的关系式![]() ,并求
,并求![]() .
.
【答案】(1)见解析;(2)![]() ;
;![]()
【解析】
(1)若选①②,结合等差数列与等比数列通项公式的基本量计算,即可求得公差和公比,即可求得数列![]() 和
和![]() 的通项公式;若选③,结合等差数列前n项和公式、等差数列与等比数列通项公式,即可求得公差和公比,即可求得数列
的通项公式;若选③,结合等差数列前n项和公式、等差数列与等比数列通项公式,即可求得公差和公比,即可求得数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)根据数列![]() 和
和![]() 的通项公式,即可由
的通项公式,即可由![]() 得m,n的关系式
得m,n的关系式![]() ,利用分组求和法即可求得
,利用分组求和法即可求得![]() .
.
(1)若选①:
设等差数列![]() 的公差为d,等比数列
的公差为d,等比数列![]() 的公比为q(
的公比为q(![]() ),
),
则![]() ,
,
解得![]() 或
或![]() (舍),
(舍),
则![]() ,
,![]() ,
,
若选②:
设等差数列![]() 的公差为d,等比数列
的公差为d,等比数列![]() 的公比为q(
的公比为q(![]() ),
),
则由![]() 得
得![]() ,
,
![]() ,又
,又![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
若选③:
设等差数列![]() 的公差为d,等比数列
的公差为d,等比数列![]() 的公比为q(
的公比为q(![]() ),
),
则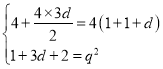 ,解得
,解得![]() 或
或![]() (舍),
(舍),
则![]() ,
,![]() .
.
(2)∵![]() ,
,
∴![]() ,即
,即![]() ,
,
![]()
![]()
![]()
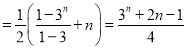 .
.

练习册系列答案
相关题目