题目内容
【题目】已知函数![]() 在
在![]() 处取得极值A,函数
处取得极值A,函数![]() ,其中
,其中![]() …是自然对数的底数.
…是自然对数的底数.
(1)求m的值,并判断A是![]() 的最大值还是最小值;
的最大值还是最小值;
(2)求![]() 的单调区间;
的单调区间;
(3)证明:对于任意正整数n,不等式![]() 成立.
成立.
【答案】(1)![]() ;
;![]() 是最小值;(2)单调递减区间是
是最小值;(2)单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ;(3)证明过程见详解.
;(3)证明过程见详解.
【解析】
(1)先对函数求导,根据题意,得到![]() ,求出
,求出![]() ,研究函数单调性,即可判断出结果;
,研究函数单调性,即可判断出结果;
(2)对函数![]() 求导,得到
求导,得到![]() ,令
,令![]() ,对其求导,研究其单调性,即可判断函数
,对其求导,研究其单调性,即可判断函数![]() 的单调性;
的单调性;
(3)先由(1)得![]() 时,
时,![]() 恒成立,令
恒成立,令![]() ,则
,则![]() ,进而求和,即可得出结果.
,进而求和,即可得出结果.
(1)因为![]() ,
,![]() ,所以
,所以![]() ,
,
又![]() 在
在![]() 处取得极值
处取得极值![]() ,
,
则![]() ,即
,即![]() ;所以
;所以![]() ,
,
由![]() 得
得![]() ;由
;由![]() 得
得![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
因此![]() 在
在![]() 处取得最小值,即
处取得最小值,即![]() 是最小值;
是最小值;
(2)由(1)得![]() ,
,
所以![]() ,
,
令![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() 恒成立,
恒成立,
因此![]() 在
在![]() 上单调递增;又
上单调递增;又![]() ,
,
所以,当![]() 时,
时,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ;
;
所以函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ;
;
(3)由(1)知,![]() ,
,
所以![]() ,当
,当![]() 时,
时,![]() 恒成立;
恒成立;
令![]() ,则
,则![]() ,
,
因此![]()
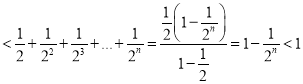 ,
,
即![]() ,
,
因此![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某汽车品牌为了了解客户对于其旗下的五种型号汽车的满意情况,随机抽取了一些客户进行回访,调查结果如下表:
汽车型号 | I | II | III | IV | V |
回访客户(人数) | 250 | 100 | 200 | 700 | 350 |
满意率 | 0.5 | 0.3 | 0.6 | 0.3 | 0.2 |
满意率是指:某种型号汽车的回访客户中,满意人数与总人数的比值.
假设客户是否满意互相独立,且每种型号汽车客户对于此型号汽车满意的概率与表格中该型号汽车的满意率相等.
(1)从所有的回访客户中随机抽取1人,求这个客户满意的概率;
(2)从I型号和V型号汽车的所有客户中各随机抽取1人,设其中满意的人数为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(3)用 “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”分别表示I, II, III, IV, V型号汽车让客户满意, “
”分别表示I, II, III, IV, V型号汽车让客户满意, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ” 分别表示I, II, III, IV, V型号汽车让客户不满意.写出方差
” 分别表示I, II, III, IV, V型号汽车让客户不满意.写出方差![]() 的大小关系.
的大小关系.