题目内容
【题目】已知数列{an}的前n项和Sn和通项an满足
.
（1）求数列{an}的通项公式；
（2）等差数列{bn}中，b1＝3a1，b2＝2，求数列{an+bn}的前n项和Tn.
【答案】（1）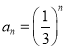
.（2）
【解析】
（1）先由数列{an}的前n项和Sn和通项an的关系式求出相邻项之间的关系，判断出数列{an}的类型，再求出通项公式；
（2）先由题设条件求出bn，再结合（1）中的an求出an+bn，最后求出Tn.
（1）当n＝1时有2S1+a1＝1＝3a1，解得
.
又∵2Sn+an＝1（n∈N*）①，∴2Sn+1+an+1＝1 ②.
由②﹣①可得：2（Sn+1﹣Sn）+an+1﹣an＝0＝2an+1+an+1﹣an，即an+1
，
所以数列{an}是以
为首项，以为公比的等比数列，∴an＝（）n.
（2）∵等差数列{bn}中，b1＝3a1＝1，b2＝2，∴bn＝n，an+bn＝（）n+n.
∴Tn＝[
]+（1+2+3+…n）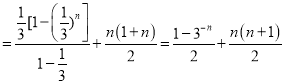
.
芒果教辅暑假天地重庆出版社系列答案
【题目】我国全面二孩政策已于2016年1月1日起正式实施．国家统计局发布的数据显示，从2012年到2017年，中国的人口自然增长率变化始终不大，在5‰上下波动（如图）．
为了了解年龄介于24岁至50岁之间的适孕夫妻对生育二孩的态度如何，统计部门按年龄分为9组，每组选取150对夫妻进行调查统计有生育二孩意愿的夫妻数，得到下表：
年龄区间 |
|
|
|
|
|
|
|
|
|
有意愿数 | 80 | 81 | 87 | 86 | 84 | 83 | 83 | 70 | 66 |
（1）设每个年龄区间的中间值为
，有意愿数为
，求样本数据的线性回归直线方程，并求该模型的相关系数
（结果保留两位小数）；
（2）从
，
，
，
，
这五个年龄段中各选出一对夫妻（能代表该年龄段超过半数夫妻的意愿）进一步调研，再从这5对夫妻中任选2对夫妻．求其中恰有一对不愿意生育二孩的夫妻的概率．
（参考数据和公式：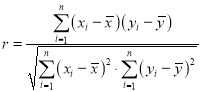
，
，
，
，
，
）
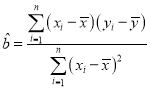【题目】某汽车品牌为了了解客户对于其旗下的五种型号汽车的满意情况，随机抽取了一些客户进行回访，调查结果如下表：
汽车型号 | I | II | III | IV | V |
回访客户（人数） | 250 | 100 | 200 | 700 | 350 |
满意率 | 0.5 | 0.3 | 0.6 | 0.3 | 0.2 |
满意率是指：某种型号汽车的回访客户中，满意人数与总人数的比值.
假设客户是否满意互相独立，且每种型号汽车客户对于此型号汽车满意的概率与表格中该型号汽车的满意率相等.
(1)从所有的回访客户中随机抽取1人，求这个客户满意的概率；
(2)从I型号和V型号汽车的所有客户中各随机抽取1人，设其中满意的人数为
，求的分布列和期望；
(3)用 “
”, “
”, “
”, “
”, “
”分别表示I, II, III, IV, V型号汽车让客户满意， “
”, “
”, “
”, “
”, “
” 分别表示I, II, III, IV, V型号汽车让客户不满意.写出方差
的大小关系.
