题目内容
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)直线![]() 为函数
为函数![]() 图象的一条切线,若对任意的
图象的一条切线,若对任意的![]() ,
,![]() 都有
都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时没有极值;当
时没有极值;当![]() 时,有极大值,极大值为
时,有极大值,极大值为![]() ;(2)
;(2)![]() .
.
【解析】
(1)求导,对参数![]() 进行分类讨论,根据导数的正负,即可判断函数的单调性,根据单调性求极值;
进行分类讨论,根据导数的正负,即可判断函数的单调性,根据单调性求极值;
(2)设出切点为![]() ,利用导数几何意义求得
,利用导数几何意义求得![]() 与
与![]() 之间的关系,将问题转化为在对应区间满足
之间的关系,将问题转化为在对应区间满足![]() ,即可求得参数范围.
,即可求得参数范围.
解:(1)∵![]() ,
,
∴函数![]() 的定义域为
的定义域为![]() .
.
∵![]() ,
,
∴![]() .
.
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为增函数,无极值;
上为增函数,无极值;
②当![]() 时,由
时,由![]() ,得
,得![]() .
.
∵![]() 时,
时,![]() ,
,![]() 为增函数,
为增函数,
![]() 时,
时,![]() ,
,![]() 为减函数,
为减函数,
∴![]() 在定义域上有极大值,极大值为
在定义域上有极大值,极大值为![]() .
.
(2)设直线![]() 与函数
与函数![]() 图象相切的切点为
图象相切的切点为![]() ,则
,则![]() .
.
∵![]() ,∴
,∴![]() .∴
.∴![]() .∴
.∴![]() .
.
又∵![]() ,
,
∴![]() .∴
.∴![]() .∴
.∴![]() .
.
∴![]() .
.
∵对任意的![]() ,
,![]() 都有
都有![]() 成立,
成立,
∴只需![]()
∵![]() ,
,
∴由![]() ,得
,得![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() 时,
时,![]() ,
,![]() 为减函数,
为减函数,
![]() 时,
时,![]() ,
,![]() 为增函数.
为增函数.
∴![]() ,即
,即![]() .
.
∵![]() 在
在![]() 上为减函数,
上为减函数,
∴![]() .
.
∴![]() .
.
即![]() .
.
设![]() ,易知
,易知![]() 在
在![]() 上为增函数.
上为增函数.
又∵![]() ,
,
∴实数![]() 的取值范围为
的取值范围为![]() .
.

【题目】某公司为抓住经济发展的契机,调查了解了近几年广告投入对销售收益的影响,在若干销售地区分别投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示),由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
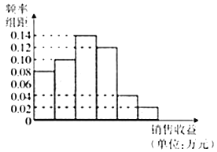
(1)根据频率分布直方图计算图中各小长方形的宽度;并估计该公司分别投入4万元广告费用之后,对应地区销售收益的平均值(以各组的区间中点值代表该组的取值);
(2)该公司按照类似的研究方法,测得另外一些数据,并整理得到如表:
广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
销售收益y(单位:万元) | 2 | 3 | 2 | 7 |
由表中的数据显示,x与y之间存在着线性相关关系,请将(1)的结果填入空白栏,根据表格中数据求出y关于x的回归真线方程![]() ,并估计该公司下一年投入广告费多少万元时,可使得销售收益达到8万元?
,并估计该公司下一年投入广告费多少万元时,可使得销售收益达到8万元?
参考公式:最小二乘法估计分别为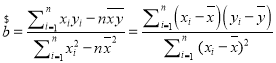 ,
,![]() .
.
【题目】某汽车品牌为了了解客户对于其旗下的五种型号汽车的满意情况,随机抽取了一些客户进行回访,调查结果如下表:
汽车型号 | I | II | III | IV | V |
回访客户(人数) | 250 | 100 | 200 | 700 | 350 |
满意率 | 0.5 | 0.3 | 0.6 | 0.3 | 0.2 |
满意率是指:某种型号汽车的回访客户中,满意人数与总人数的比值.
假设客户是否满意互相独立,且每种型号汽车客户对于此型号汽车满意的概率与表格中该型号汽车的满意率相等.
(1)从所有的回访客户中随机抽取1人,求这个客户满意的概率;
(2)从I型号和V型号汽车的所有客户中各随机抽取1人,设其中满意的人数为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(3)用 “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”分别表示I, II, III, IV, V型号汽车让客户满意, “
”分别表示I, II, III, IV, V型号汽车让客户满意, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ” 分别表示I, II, III, IV, V型号汽车让客户不满意.写出方差
” 分别表示I, II, III, IV, V型号汽车让客户不满意.写出方差![]() 的大小关系.
的大小关系.