Question

方程mx+ny²=0与mx²+ny²=1，（m，n∈R）且mn≠0在同一坐标系中所表示的曲线可能是（　　）

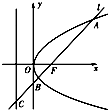
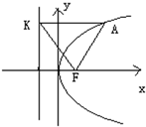
A．

B．

C．

D．

Answer 1

方程mx+ny²=0 即 y²=-

m

n

x，表示抛物线，方程mx²+ny²=1（mn≠0）表示椭圆或双曲线．
当m和n同号时，抛物线开口向左，方程mx²+ny²=1（mn≠0）表示椭圆，无符合条件的选项．
当m和n异号时，抛物线 y²=-

m

n

x开口向右，方程mx²+ny²=1表示双曲线，
故选：C．