Question

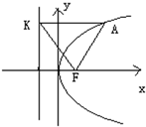
如图，抛物线y²=4x的焦点为F，准线为l，经过F且斜率为

3

的直线与抛物线在x轴上方的部分相交于点A，AK⊥l，垂足为K，则△AKF的面积是______．

Answer 1

由抛物线的定义可得AF=AK，∵AF的斜率等于

3

，∴AF的倾斜角等于60°，∵AK⊥l，
∴∠FAK=60°，故△AKF为等边三角形．又焦点F（1，0），AF的方程为 y-0=

3

（x-1），
设A（m，

3

m-

3

），m＞1，由AF=AK 得

(m-1)2+( 3 m- 3 )2

=m+1，
∴m=3，故等边三角形△AKF的边长AK=m+1=4，
∴△AKF的面积是

1

2

×4×4sin60°=4

3

，
故答案为4

3

．