题目内容
6.在三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2$\sqrt{3}$,VC=1,则二面角V-AB-C的平面角度数是60°.分析 取AB的中点为D,连接VD,CD,则∠VDC是二面角V-AB-C的平面角,从而可得结论.
解答  解:取AB的中点为D,连接VD,CD.
解:取AB的中点为D,连接VD,CD.
∵VA=VB,∴AB⊥VD;
同理AB⊥CD.
所以∠VDC是二面角V-AB-C的平面角.
由题设可知VD=CD=1,即∠VDC=60°.
故二面角V-AB-C的大小为60°.
故答案为:60°.
点评 本题考查面面角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
11.执行如图所示的程序框图,若输出b=3,则输入的实数a的取值范围是( )
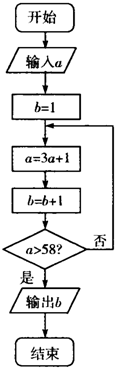

| A. | (19,+∞) | B. | (8,19] | C. | (6,19] | D. | ($\frac{5}{3}$,6] |