题目内容
18.已知数列{an}的首项a1=1,前n项和为Sn,且对任意的正整数n都有2an+1+Sn=2(1)证明:数列{an}是等比数列;
(2)是否存在正整数m,n,使得$\frac{{S}_{n+1}-m}{{S}_{n}-m}$>1+am+2成立?若存在.求出符合条件的有序实数对(m,n),若不存在,请说明理由.
分析 (1)通过2an+1+Sn=2与2an+2+Sn+1=2作差、整理得an+2=$\frac{1}{2}$an+1,进而可知数列{an}是以1为首项、$\frac{1}{2}$为公比的等比数列;
(2)通过(1)可知Sn=2-$\frac{1}{{2}^{n-1}}$、an=$\frac{1}{{2}^{n-1}}$,通过化简可知$\frac{{S}_{n+1}-m}{{S}_{n}-m}$=1+$\frac{1}{{2}^{n+1}-m•{2}^{n}-2}$,进而$\frac{{S}_{n+1}-m}{{S}_{n}-m}$>1+am+2成立等价于$\frac{1}{{2}^{n+1}-m•{2}^{n}-2}$>$\frac{1}{{2}^{m+1}}$,从而确定m=1,化简计算即得结论.
解答 (1)证明:∵2an+1+Sn=2,
∴2an+2+Sn+1=2,
两式相减得:2an+2+an+1-2an+1=0,
整理得:an+2=$\frac{1}{2}$an+1,
又∵2a2+a1=2,即2a2=2-a1=2-1=1=a1满足上式,
∴数列{an}是以1为首项、$\frac{1}{2}$为公比的等比数列;
(2)结论:存在符合条件的所有有序实数对(m,n)为:(1,1),(1,2).
理由如下:
由(1)可知,Sn=$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$=2-$\frac{1}{{2}^{n-1}}$,
∴$\frac{{S}_{n+1}-m}{{S}_{n}-m}$=$\frac{{S}_{n}+{a}_{n+1}-m}{{S}_{n}-m}$=1+$\frac{{a}_{n+1}}{{S}_{n}-m}$=1+$\frac{\frac{1}{{2}^{n}}}{2-\frac{1}{{2}^{n-1}}-m}$=1+$\frac{1}{{2}^{n+1}-m•{2}^{n}-2}$,
∴$\frac{{S}_{n+1}-m}{{S}_{n}-m}$>1+am+2成立等价于$\frac{1}{{2}^{n+1}-m•{2}^{n}-2}$>am+2=$\frac{1}{{2}^{m+1}}$,
∴0<2n+1-m•2n-2<2m+1,(*)
∴(2-m)2n<2(1+2m),
∴(2-m)2n-1<1+2m,
当m≥2时,$\frac{1}{{2}^{n+1}-m•{2}^{n}-2}$<0,显然不满足题意,
∴m=1,
∴(*)式即为:0<2n+1-2n-2<22,
整理得:0<2n<6,
∴n=1,2,
综上,存在符合条件的所有有序实数对(m,n)为:(1,1),(1,2).
点评 本题考查了等比关系的确定,考查了等比数列的和,训练了与数列有关的存在性问题的判定方法,注意解题方法的积累,属于难题.

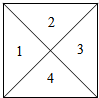 如图,有4个编号为1、2、3、4的小三角形,要在每一个小三角形中涂上红、黄、蓝、白、黑五种颜色中的一种,并且相邻的小三角形颜色不同,共有多少种不同的涂色方法?
如图,有4个编号为1、2、3、4的小三角形,要在每一个小三角形中涂上红、黄、蓝、白、黑五种颜色中的一种,并且相邻的小三角形颜色不同,共有多少种不同的涂色方法?