题目内容
1.已知椭圆的右焦点为F,A为椭圆上异于椭圆左右顶点的任意一点,且B与A关于原点O对称,直线AF交椭圆于另外一点C,直线BF交椭圆于另外一点D,则直线AD与BC的交点M的轨迹方程为x=$\frac{{a}^{2}}{c}$.分析 利用设而不求的思想,设出A,B的坐标没求出直线DA,DB的斜率即可得到结论
解答 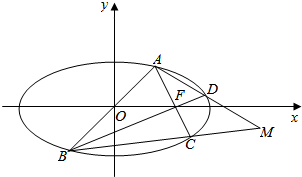 解:如图,
解:如图,
设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,F(c,0),
设A(x1,y1),D(x2,y2),则B(-x1,-y1),
∴kBD=kBF=$\frac{{y}_{1}}{{x}_{1}+c}$,
∵kBD•kAD=$\frac{{{y}_{2}}^{2}-{{y}_{1}}^{2}}{{{x}_{2}}^{2}-{{x}_{1}}^{2}}$=-$\frac{{b}^{2}}{{a}^{2}}$,
∴kAD=-$\frac{{b}^{2}}{{a}^{2}}$•$\frac{{x}_{1}+c}{{y}_{1}}$
∴直线AD的方程为y-y1=-$\frac{{b}^{2}}{{a}^{2}}$•$\frac{{x}_{1}+c}{{y}_{1}}$(x-x1)①
同理,直线BC的方程为y+y1=-$\frac{{b}^{2}}{{a}^{2}}$•$\frac{{x}_{1}-c}{{y}_{1}}$(x+x1)②
由②-①整理得x=$\frac{{a}^{2}}{c}$
∴直线AD与BC的交点M在定直线x=$\frac{{a}^{2}}{c}$上.
故答案为:x=$\frac{{a}^{2}}{c}$.
点评 本题主要考查椭圆方程以及直线和椭圆方程的位置关系的应用,利用设而不求的思想以以及点差法是解决本题的关键.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
4.已知在△ABC中,a、b、c分别是三内角∠A、∠B、∠C的对边,且$\frac{\sqrt{2}b}{a-\sqrt{2}b}$=$\frac{sin2B}{sinA-sin2B}$,则∠B=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{3π}{4}$ |
11.已知函数f(x)=2x,曲线C1与g1(x)=f(x)-$\frac{1}{a}$f(-x)的图象关于原点对称,曲线C2为g2(x)=f(x)-af(-x)的图象向右平移2个单位后所得,过x轴上的动点M(t,0)作垂直于x轴的直线分别交曲线C1、C2于A、B两点,若函数h(t)=yA-yB+xA-xB的最小值为m且m>$\sqrt{7}$,则实数a的取值范围是( )
| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{2}$,4) | C. | ($\frac{1}{4}$,2) | D. | (2,4) |