题目内容
15.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且椭圆的短轴长为2.(1)若P是该椭圆上的一个动点,求函数z=x2+y2-3的最值,并指出取得最值时,点P的位置;
(2)过定点M(0,2)的直线l与椭圆交于不同的两点A,B,且∠AOB为锐角(其中O为坐标原点),求直线l的斜率k的取值范围.
分析 (1)根据椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且椭圆的短轴长为2,求出a,b,求得椭圆方程,再求出函数z=x2+y2-3的最值,并指出取得最值时,点P的位置;
(2)设出直线方程,与已知椭圆联立方程组,运用设而不求韦达定理求出根的关系,求出k的取值范围.
解答 解:(1)∵椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且椭圆的短轴长为2.
∴a=2,b=1
∴椭圆方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$,
z=x2+y2-3=z=x2+1-$\frac{1}{4}$x2-3=$\frac{3}{4}$x2-2,
∴x=0时,z取得最小值-2,P为椭圆的短轴顶点;x=±2时,z取得最大值1,P为椭圆的长轴顶点;
(2)显然直线x=0不满足题设条件,
可设直线l:y=kx+2,A(x1,y1),B(x2,y2),
代入椭圆方程,消去y,整理得:(k2+$\frac{1}{4}$)x2+4kx+3=0
∴x1+x2=-$\frac{4k}{{k}^{2}+\frac{1}{4}}$,x1x2=$\frac{3}{{k}^{2}+\frac{1}{4}}$
由△=(4k)2-4(k2+$\frac{1}{4}$)×3=4k2-3>0得:k<-$\frac{\sqrt{3}}{2}$或k>$\frac{\sqrt{3}}{2}$①
又0°<∠AOB<90°?cos∠AOB>0,
cos∠AOB>0?$\overrightarrow{OA}$•$\overrightarrow{OB}$>0
∴x1x2+y1y2>0
又y1y2=(kx1+2)(kx2+2)
=k2x1x2+2k(x1+x2)+4
=k2×$\frac{3}{{k}^{2}+\frac{1}{4}}$+2k×(-$\frac{4k}{{k}^{2}+\frac{1}{4}}$ )+4=$\frac{-{k}^{2}+1}{{k}^{2}+\frac{1}{4}}$
∴$\frac{3}{{k}^{2}+\frac{1}{4}}$+$\frac{-{k}^{2}+1}{{k}^{2}+\frac{1}{4}}$>0
即k2<4,∴-2<k<2②
故由①、②得:
-2<k<-$\frac{\sqrt{3}}{2}$或$\frac{\sqrt{3}}{2}$<k<2.
点评 本题主要考查直线、椭圆、平面向量的数量积等基础知识,以及综合应用数学知识解决问题及推理计算能力.本题为中档题,需要熟练运用设而不求韦达定理.

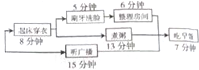
| A. | 22分钟 | B. | 26分钟 | C. | 28分钟 | D. | 32分钟 |
| A. | 1007 | B. | -1007 | C. | 2014 | D. | -2014 |
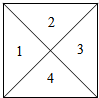 如图,有4个编号为1、2、3、4的小三角形,要在每一个小三角形中涂上红、黄、蓝、白、黑五种颜色中的一种,并且相邻的小三角形颜色不同,共有多少种不同的涂色方法?
如图,有4个编号为1、2、3、4的小三角形,要在每一个小三角形中涂上红、黄、蓝、白、黑五种颜色中的一种,并且相邻的小三角形颜色不同,共有多少种不同的涂色方法?