题目内容
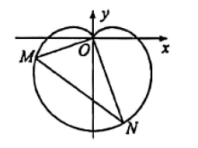
【题目】已知椭圆![]() 的长轴为
的长轴为![]() ,
,![]() 分别为椭圆C的左、右顶点,P是椭圆C上异于
分别为椭圆C的左、右顶点,P是椭圆C上异于![]() 的动点,且
的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆C的方程;
(2)过点![]() 的直线l交椭圆C于
的直线l交椭圆C于![]() 两点,D为椭圆上一点,O为坐标原点,且满足
两点,D为椭圆上一点,O为坐标原点,且满足![]() ,其中
,其中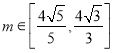 ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
【答案】(1)![]() ;(2)
;(2) .
.
【解析】
(1)易知![]() ,当P点为椭圆上顶点时
,当P点为椭圆上顶点时![]() 的面积最大,求出
的面积最大,求出![]() 的值,然后写出方程即可;
的值,然后写出方程即可;
(2)设直线方程为![]() ,联立直线和椭圆方程得
,联立直线和椭圆方程得![]() ,
,
设![]() ,
,![]() ,
,![]() 由韦达定理得出
由韦达定理得出![]() 和
和![]() 的值,再由
的值,再由![]() ,得
,得![]() 点坐标,代入椭圆方程得到
点坐标,代入椭圆方程得到![]() 与
与![]() 的关系,继而求出
的关系,继而求出![]() 的范围.
的范围.
(1)因为椭圆![]() 的长轴为
的长轴为![]() ,所以
,所以![]() ,
,
![]() ,因为
,因为![]() 面积的最大值为
面积的最大值为![]() ,
,
所以当P点为椭圆上顶点时面积最大,![]() ,
,
解得![]() ,故所求的椭圆方程为
,故所求的椭圆方程为![]() ;
;
(2)由题意可知该直线的斜率存在,设其方程为![]() ,
,
由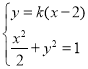 得
得![]() ,
,
∴![]() ,得
,得![]() ,
,
设![]() ,
,![]() ,
,![]() ,则
,则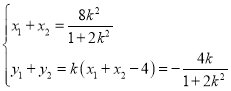 ,
,
由![]() ,得
,得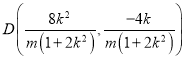 ,
,
代入椭圆方程得![]() ,
,
由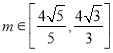 ,得
,得![]() 且
且![]() ,
,
所以![]() ,
,
∴ .
.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
【题目】某高校健康社团为调查本校大学生每周运动的时长,随机选取了80名学生,调查他们每周运动的总时长(单位:小时),按照![]()
![]()
![]()
![]()
![]()
![]() 共6组进行统计,得到男生、女生每周运动的时长的统计如下(表1、2),规定每周运动15小时以上(含15小时)的称为“运动合格者”,其中每周运动25小时以上(含25小时)的称为“运动达人”.
共6组进行统计,得到男生、女生每周运动的时长的统计如下(表1、2),规定每周运动15小时以上(含15小时)的称为“运动合格者”,其中每周运动25小时以上(含25小时)的称为“运动达人”.
表1:男生
时长 |
|
|
|
|
|
|
人数 | 2 | 8 | 16 | 8 | 4 | 2 |
表2:女生
时长 |
|
|
|
|
|
|
人数 | 0 | 4 | 12 | 12 | 8 | 4 |
(1)从每周运动时长不小于20小时的男生中随机选取2人,求选到“运动达人”的概率;
(2)根据题目条件,完成下面![]() 列联表,并判断能否有99%的把握认为本校大学生是否为“运动合格者”与性别有关.
列联表,并判断能否有99%的把握认为本校大学生是否为“运动合格者”与性别有关.
每周运动的时长小于15小时 | 每周运动的时长不小于15小时 | 总计 | |
男生 | |||
女生 | |||
总计 | |||
参考公式: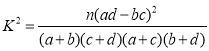 ,其中
,其中![]() .
.
参考数据:
| 0.40 | 0.25 | 0.10 | 0.010 |
| 0.708 | 1.323 | 2.706 | 6.635 |