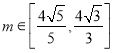题目内容
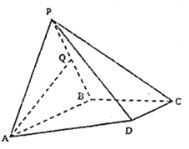
【题目】在三棱锥P—ABC中,PB![]() 平面ABC,AB
平面ABC,AB![]() BC,AB=PB=2,BC=2
BC,AB=PB=2,BC=2![]() ,E、G分别为PC、PA的中点.
,E、G分别为PC、PA的中点.
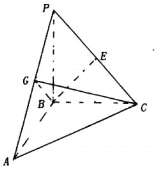
(1)求证:平面BCG![]() 平面PAC;
平面PAC;
(2)假设在线段AC上存在一点N,使PN![]() BE,求
BE,求![]() 的值;
的值;
(3)在(2)的条件下,求直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由![]() ,
,![]() ,得
,得![]() 平面
平面![]() ,即可得到本题的结论;(2)由N为线段AC一点,可设为
,即可得到本题的结论;(2)由N为线段AC一点,可设为![]() ,得
,得![]() ,又由,
,又由,![]() 可确定
可确定![]() 的取值,从而可得到本题答案;(3)求出平面
的取值,从而可得到本题答案;(3)求出平面![]() 的法向量
的法向量![]() ,然后套入公式
,然后套入公式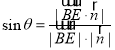 ,即可得到本题答案.
,即可得到本题答案.
(1) 因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,则
,则![]() ①,
①,
又![]() ,
,![]() 为等腰直角三角形,G为斜边
为等腰直角三角形,G为斜边![]() 的中点,所以
的中点,所以![]() ②,
②,
又![]() ,所以
,所以![]() 平面
平面![]() ,因
,因![]() 平面
平面![]() ,
,
则有平面![]() 平面
平面 ![]() ;
;
(2)分别以![]() 为
为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
那么![]() ,因此
,因此![]() ,
,![]() ,设
,设![]() ,那么
,那么![]() ,
,
由![]() ,得
,得![]() ,解得
,解得![]() .
.
因此![]() ,因此
,因此![]() ;
;
(3)由(2)知![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,则
,则
![]() ,即
,即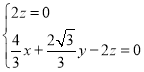 ,
,
令![]() ,得
,得![]() ,
,![]() 因此
因此![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,那么
,那么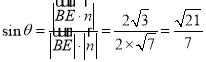 .
.

练习册系列答案
相关题目
【题目】某校实行选科走班制度,张毅同学的选择是物理生物政治这三科,且物理在 A 层班级,生物在 B 层班级,该校周一上午课程安排如下表所示,张毅选择三个科目的课各上一节, 另外一节上自习,则他不同的选课方法有( )
第一节 | 第二节 | 第三节 | 第四节 |
地理 B 层 2 班 | 化学 A 层 3 班 | 地理 A 层 1 班 | 化学 A 层 4 班 |
生物 A 层 1 班 | 化学 B 层 2 班 | 生物 B 层 2 班 | 历史 B 层 1 班 |
物理 A 层 1 班 | 生物 A 层 3 班 | 物理 A 层 2 班 | 生物 A 层 4 班 |
物理 B 层 2 班 | 生物 B 层 1 班 | 物理 B 层 1 班 | 物理 A 层 4 班 |
政治 1 班 | 物理 A 层 3 班 | 政治 2 班 | 政治 3 班 |
A.8 种B.10 种C.12 种D.14 种