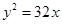题目内容
已知过点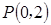 的直线
的直线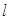 与抛物线
与抛物线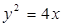 交于
交于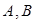 两点,
两点,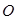 为坐标原点.
为坐标原点.
(1)若以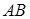 为直径的圆经过原点
为直径的圆经过原点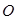 ,求直线
,求直线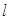 的方程;
的方程;
(2)若线段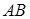 的中垂线交
的中垂线交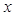 轴于点
轴于点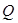 ,求
,求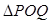 面积的取值范围.
面积的取值范围.
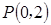 的直线
的直线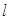 与抛物线
与抛物线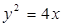 交于
交于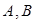 两点,
两点,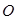 为坐标原点.
为坐标原点.(1)若以
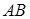 为直径的圆经过原点
为直径的圆经过原点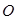 ,求直线
,求直线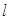 的方程;
的方程;(2)若线段
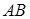 的中垂线交
的中垂线交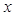 轴于点
轴于点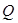 ,求
,求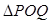 面积的取值范围.
面积的取值范围.解:(1)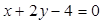 (2)
(2)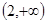 。
。
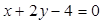 (2)
(2)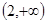 。
。试题分析:
思路分析:(1)通过分析已知条件,确定直线
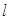 的斜率存在,故可设直线
的斜率存在,故可设直线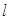 方程为
方程为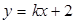 ,通过联立方程组
,通过联立方程组 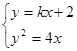 ,消去
,消去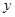 ,应用韦达定理及
,应用韦达定理及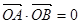 ,建立k的方程,求解。
,建立k的方程,求解。(2)通过设线段
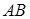 的中点坐标为
的中点坐标为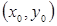
确定线段
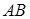 的中垂线方程为
的中垂线方程为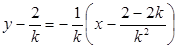 ,
,将
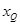 用k表示,
用k表示,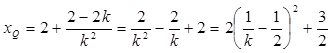 ,
,利用二次函数的图象和性质,得到
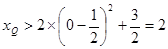 ,进一步确定三角形面积的最值。
,进一步确定三角形面积的最值。解:(1)依题意可得直线
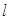 的斜率存在,设为
的斜率存在,设为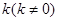 ,
,则直线
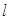 方程为
方程为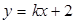 1分
1分联立方程
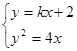 ,消去
,消去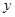 ,并整理得
,并整理得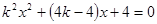 2分
2分则由
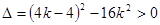 ,得
,得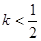
设
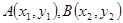 ,则
,则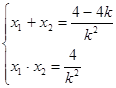 4分
4分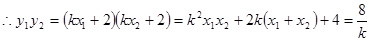 5分
5分 以
以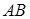 为直径的圆经过原点
为直径的圆经过原点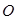
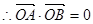
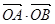
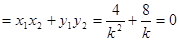 ,解得
,解得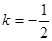 6分
6分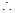 直线
直线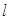 的方程为
的方程为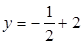 ,即
,即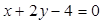 7分
7分(2)设线段
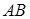 的中点坐标为
的中点坐标为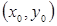
由(1)得
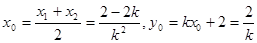 8分
8分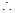 线段
线段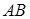 的中垂线方程为
的中垂线方程为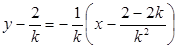 9分
9分令
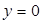 ,得
,得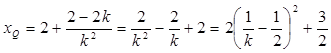 11分
11分又由(1)知
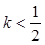 ,且
,且
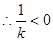 或
或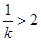
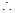
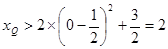 ,
,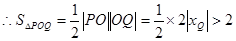 13分
13分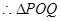 面积的取值范围为
面积的取值范围为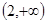 14分
14分点评:中档题,确定抛物线的标准方程,一般利用“待定系数法”,涉及直线与抛物线的位置关系,往往通过联立方程组,应用韦达定理,简化解题过程。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
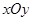 中,已知曲线
中,已知曲线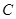 上任意一点到点
上任意一点到点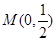 的距离与到直线
的距离与到直线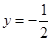 的距离相等.
的距离相等.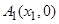 ,
,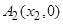 是
是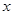 轴上的两点
轴上的两点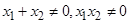 ,过点
,过点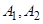 分别作
分别作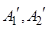 ,直线
,直线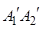 与x轴交于点
与x轴交于点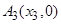 ,这样就称
,这样就称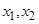 确定了
确定了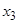 .同样,可由
.同样,可由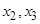 确定了
确定了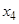 .现已知
.现已知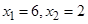 ,求
,求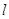 经过抛物线
经过抛物线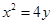 的焦点,且与抛物线交于
的焦点,且与抛物线交于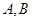 两点,点
两点,点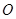 为坐标原点.
为坐标原点.
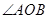 为钝角.
为钝角.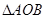 的面积为
的面积为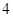 ,求直线
,求直线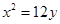 上,且与直线
上,且与直线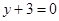 相切,则此圆恒过定点( )
相切,则此圆恒过定点( )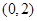
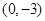
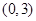
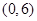
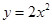 的焦点坐标是____________.
的焦点坐标是____________.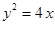 ,过
,过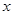 轴上一点
轴上一点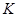 的直线与抛物线交于点
的直线与抛物线交于点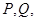 两点。
两点。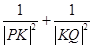 为常数,并确定
为常数,并确定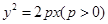 的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为
的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为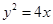 或
或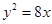
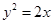 或
或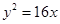
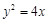 的焦点,
的焦点,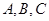 为抛物线上不同的三点,点
为抛物线上不同的三点,点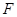 是△ABC的重心,
是△ABC的重心,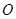 为坐标原点,△
为坐标原点,△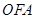 、△
、△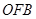 、△
、△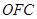 的面积分别为
的面积分别为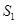 、
、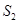 、
、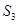 ,则
,则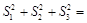 ( )
( )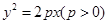 上一点到焦点和抛物线对称轴的距离分别为
上一点到焦点和抛物线对称轴的距离分别为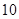 和
和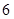 ,则抛物线方程为( )
,则抛物线方程为( )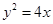
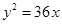
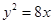 或
或