题目内容
已知抛物线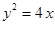 ,过
,过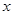 轴上一点
轴上一点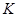 的直线与抛物线交于点
的直线与抛物线交于点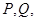 两点。
两点。
证明,存在唯一一点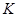 ,使得
,使得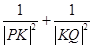 为常数,并确定
为常数,并确定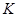 点的坐标。
点的坐标。
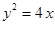 ,过
,过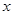 轴上一点
轴上一点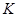 的直线与抛物线交于点
的直线与抛物线交于点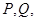 两点。
两点。证明,存在唯一一点
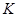 ,使得
,使得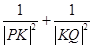 为常数,并确定
为常数,并确定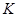 点的坐标。
点的坐标。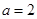 时,
时,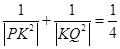 为定值,此时
为定值,此时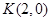 。
。试题分析:设
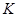 (
(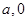 ),过
),过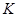 点直线方程为
点直线方程为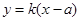 ,交抛物线于
,交抛物线于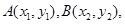 联立方程组
联立方程组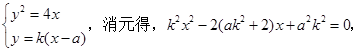
由韦达定理得
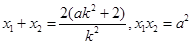 …5分
…5分使用,
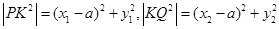 7分
7分即
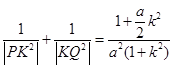 , 12分
, 12分所以,
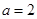 时,
时,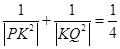 为定值,此时
为定值,此时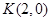 。 17分
。 17分点评:中档题,涉及直线与圆锥曲线位置关系问题,往往通过联立方程组,应用韦达定理,简化解题过程 。

练习册系列答案
相关题目
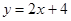 与抛物线
与抛物线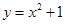 所围成封闭图形的面积是( )
所围成封闭图形的面积是( )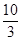
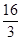
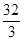
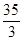
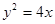 图像上一点
图像上一点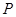 引抛物线准线的垂线,垂足为
引抛物线准线的垂线,垂足为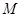 ,且
,且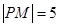 ,设抛物线焦点为
,设抛物线焦点为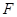 ,则
,则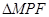 的面积为( )
的面积为( )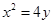 上一点P到焦点
上一点P到焦点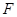 的距离是
的距离是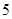 ,则点P的横坐标是_____.
,则点P的横坐标是_____.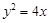 的焦点为
的焦点为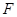 ,点
,点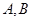 在抛物线上,且
在抛物线上,且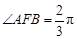 ,弦
,弦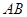 中点
中点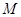 在准线
在准线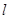 上的射影为
上的射影为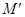 ,则
,则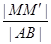 的最大值为( )
的最大值为( )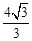
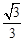
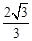
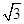
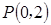 的直线
的直线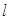 与抛物线
与抛物线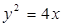 交于
交于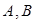 两点,
两点,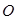 为坐标原点.
为坐标原点.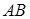 为直径的圆经过原点
为直径的圆经过原点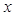 轴于点
轴于点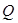 ,求
,求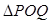 面积的取值范围.
面积的取值范围.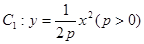 的焦点与双曲线
的焦点与双曲线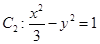 的右焦点的连线交
的右焦点的连线交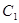 于第一象限的点
于第一象限的点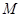 ,若
,若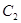 的一条渐近线,则
的一条渐近线,则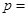 ( )
( )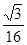
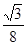

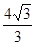
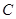 的顶点为原点,其焦点
的顶点为原点,其焦点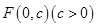 到直线
到直线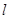 :
: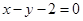 的距离为
的距离为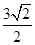 .设
.设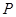 为直线
为直线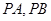 ,其中
,其中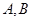 为切点.
为切点.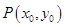 为直线
为直线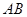 的方程;
的方程;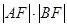 的最小值.
的最小值.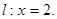 动圆M与定圆
动圆M与定圆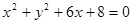 外切且与直线
外切且与直线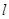 相切.
相切.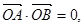 求证直线AB过一定点,并求出定点的坐标.
求证直线AB过一定点,并求出定点的坐标.