题目内容
15．已知集合P={x|x2-2x≥0}，Q={x|1＜x≤2}，则（∁RP）∩Q=（ ）| A． | [0，1） | B． | （0，2] | C． | （1，2） | D． | [1，2] |
分析 求出P中不等式的解集确定出P，求出P补集与Q的交集即可．
解答 解：由P中不等式变形得：x（x-2）≥0，
解得：x≤0或x≥2，即P=（-∞，0]∪[2，+∞），
∴∁RP=（0，2），
∵Q=（1，2]，
∴（∁RP）∩Q=（1，2），
故选：C．
点评 此题考查了交、并、补集的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
5．某中学初中部共有110名教师，高中部共有150名教师，其性别比例如图所示，则该校女教师的人数为（ ）
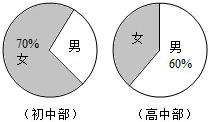
| A． | 93 | B． | 123 | C． | 137 | D． | 167 |
6．已知集合A={x|-1＜x＜2}，B={x|0＜x＜3}，则A∪B=（ ）
| A． | （-1，3） | B． | （-1，0） | C． | （0，2） | D． | （2，3） |
3．设x∈R，则“|x-2|＜1”是“x2+x-2＞0”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
20．
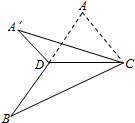如图，已知△ABC，D是AB的中点，沿直线CD将△ACD折成△A′CD，所成二面角A′-CD-B的平面角为α，则（ ）
如图，已知△ABC，D是AB的中点，沿直线CD将△ACD折成△A′CD，所成二面角A′-CD-B的平面角为α，则（ ）| A． | ∠A′DB≤α | B． | ∠A′DB≥α | C． | ∠A′CB≤α | D． | ∠A′CB≥α |
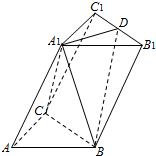如图，在三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=2，A1A=4，A1在底面ABC的射影为BC的中点，D是B1C1的中点．
6．
点（x，y）是如图所示的坐标平面的可行域内（阴影部分且包括边界）的任意一点，若目标函数z=x+ay取得最小值的最优解有无数个，则$\frac{y}{x-a}$的最大值是（ ）
点（x，y）是如图所示的坐标平面的可行域内（阴影部分且包括边界）的任意一点，若目标函数z=x+ay取得最小值的最优解有无数个，则$\frac{y}{x-a}$的最大值是（ ）| A． | $\frac{2}{3}$ | B． | $\frac{2}{5}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{4}$ |
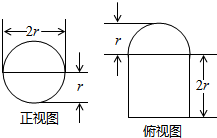圆柱被一个平面截去一部分后与半球（半径为r）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示．若该几何体的表面积为16+20π，则r=（ ）