题目内容
【题目】已知椭圆 ![]() 的左顶点和上顶点分别为A、B,左、右焦点分别是F1 , F2 , 在线段AB上有且只有一个点P满足PF1⊥PF2 , 则椭圆的离心率为( )
的左顶点和上顶点分别为A、B,左、右焦点分别是F1 , F2 , 在线段AB上有且只有一个点P满足PF1⊥PF2 , 则椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:依题意,作图如下: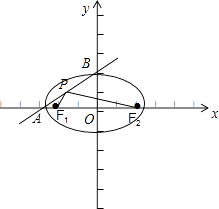
由A(﹣a,0),B(0,b),F1(﹣c,0),F2(c,0),
可得直线AB的方程为: ![]() +
+ ![]() =1,整理得:bx﹣ay+ab=0,
=1,整理得:bx﹣ay+ab=0,
设直线AB上的点P(x,y),则bx=ay﹣ab,
x= ![]() y﹣a,
y﹣a,
由PF1⊥PF2 ,
∴ ![]()
![]() =(﹣c﹣x,﹣y)(c﹣x,﹣y)=x2+y2﹣c2
=(﹣c﹣x,﹣y)(c﹣x,﹣y)=x2+y2﹣c2
=( ![]() y﹣a)2+y2﹣c2 ,
y﹣a)2+y2﹣c2 ,
令f(y)=( ![]() y﹣a)2+y2﹣c2 ,
y﹣a)2+y2﹣c2 ,
则f′(y)=2( ![]() y﹣a)
y﹣a) ![]() +2y,
+2y,
由f′(y)=0得:y= ![]() ,于是x=﹣
,于是x=﹣ ![]() ,
,
∴ ![]()
![]() =(﹣
=(﹣ ![]() )2+(
)2+( ![]() )2﹣c2=0,
)2﹣c2=0,
整理得: ![]() =c2 , 又b2=a2﹣c2 , e2=
=c2 , 又b2=a2﹣c2 , e2= ![]() ,
,
∴e4﹣3e2+1=0,
∴e2= ![]() ,又椭圆的离心率e∈(0,1),
,又椭圆的离心率e∈(0,1),
∴e2= ![]() =(
=( ![]() )2 ,
)2 ,
可得e= ![]() ,
,
故选:D.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目