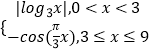题目内容
【题目】在平面直角坐标系![]() 中,将曲线
中,将曲线![]() 上的所有点横坐标伸长为原来的
上的所有点横坐标伸长为原来的![]() 倍,纵坐标伸长为原来的2倍后,得到曲线
倍,纵坐标伸长为原来的2倍后,得到曲线![]() ,在以
,在以![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出曲线![]() 的参数方程和直线
的参数方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离
的距离![]() 最大,并求出此最大值.
最大,并求出此最大值.
【答案】(1)参数方程为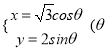 为参数),
为参数),![]() (2)
(2)![]() 取最大值
取最大值![]() ,点
,点![]() 的坐标是
的坐标是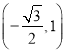
【解析】试题分析:(1)先求出曲线![]() 的普通方程,从而可写出曲线
的普通方程,从而可写出曲线![]() 的参数方程,利用极坐标与直角坐标方程的互化公式,即可求出直线
的参数方程,利用极坐标与直角坐标方程的互化公式,即可求出直线![]() 的直角坐标方程;(2)根据参数方程设出点
的直角坐标方程;(2)根据参数方程设出点![]() 坐标,得到直线
坐标,得到直线![]() 的距离
的距离![]() 的表达式,然后根据三角函数的有界性可求解最大值,并求出最大值时的
的表达式,然后根据三角函数的有界性可求解最大值,并求出最大值时的![]() 坐标.
坐标.
试题解析:(1)由题意知,曲线C2方程为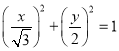 ,参数方程为
,参数方程为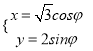 (φ为参数).直线l的直角坐标方程为2x-y-6=0.
(φ为参数).直线l的直角坐标方程为2x-y-6=0.
(2)设P(![]() cos φ,2sin φ),则点P到直线l的距离为
cos φ,2sin φ),则点P到直线l的距离为
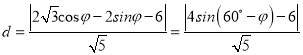 .
.
∴当sin(60°-φ)=-1时,d取最大值![]() ,此时取φ=150°,点P坐标是
,此时取φ=150°,点P坐标是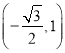 .
.

练习册系列答案
相关题目