题目内容
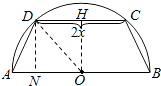
【题目】如图，有一块半径为2的半圆形纸片，计划剪裁成等腰梯形ABCD的形状，它的下底AB是⊙O的直径，上底CD的端点在圆周上，设CD=2x，梯形ABCD的周长为y． 
（1）求出y关于x的函数f（x）的解析式；
（2）求y的最大值，并指出相应的x值．
【答案】
（1）解：作OH，DN分别垂直DC，AB交于H，N，
连结OD．由圆的性质，H是中点，设OH=h，
h= 
．
又在直角△AND中，AD= 
= 
=2 
，
∴y=f（x）=AB+2AD+DC=4+2x+4 ，其定义域是（0，2）
（2）解：令t= ，则t∈（0， 
），且x=2﹣t2，
∴y=4+2（2﹣t2）+4t=﹣2（t﹣1）2+10，
当t=1，即x=1时，y的最大值是10
【解析】（1）作OH，DN分别垂直DC，AB交于H，N，连结OD，求出OH，又在直角△AND中，进一步求出AD，从而求出梯形ABCD的周长y与x间的函数解析式，根据AD＞0，AN＞0，CD＞0可求出定义域；（2）利用二次函数在给定区间上求出最值的知识可求出函数的最大值．
【考点精析】通过灵活运用函数的最值及其几何意义，掌握利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值即可以解答此题．
练习册系列答案
相关题目
