题目内容
13.由函数y=x2的图象与直线y=2x围成的图形的面积是$\frac{4}{3}$.分析 联立解曲线y=x2及直线y=2x,得它们的交点是O(0,0)和A(2,2),由此可得两个图象围成的面积等于函数y=2x-x2在[0,2]上的积分值,根据定积分计算公式加以计算,即可得到所求面积.
解答  解:由曲线y=x2与直线y=2x,解得交点为O(0,0)和A(2,2)
解:由曲线y=x2与直线y=2x,解得交点为O(0,0)和A(2,2)
因此,曲线y=x2及直线y=2x所围成的封闭图形的面积是
S=${∫}_{0}^{2}$(2x-x2)dx=(x2-$\frac{1}{3}$x3)${|}_{0}^{2}$=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题给出曲线y=x2及直线y=2x,求它们围成的图形的面积,着重考查了定积分的几何意义和定积分计算公式等知识,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.若复数z满足(1-i)z=i,其中i为虚数单位,则在复平面上复数z对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.已知$sin(π+α)=\frac{1}{3}$,则cos2α=( )
| A. | $\frac{7}{9}$ | B. | $\frac{8}{9}$ | C. | $-\frac{7}{9}$ | D. | $\frac{{4\sqrt{2}}}{9}$ |
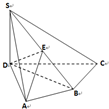 如图,在四棱锥S-ABCD中,SD⊥底面ABCD,AD⊥CD,BC⊥BD,∠BAD=60°,SD=AD=AB,E是SB的中点.
如图,在四棱锥S-ABCD中,SD⊥底面ABCD,AD⊥CD,BC⊥BD,∠BAD=60°,SD=AD=AB,E是SB的中点.