题目内容
3. 如图,在四棱锥S-ABCD中,SD⊥底面ABCD,AD⊥CD,BC⊥BD,∠BAD=60°,SD=AD=AB,E是SB的中点.
如图,在四棱锥S-ABCD中,SD⊥底面ABCD,AD⊥CD,BC⊥BD,∠BAD=60°,SD=AD=AB,E是SB的中点.(1)证明:BC⊥DE.
(2)证明:平面SBC⊥平面ADE.
(3)求二面角B-SC-D的正弦值.
分析 (1)由线面垂直的性质得到BC⊥SD,再由已知BC⊥BD,利用线面垂直的判断BC⊥面SBD,进一步得到BC⊥DE;
(2)由已知可得△ABD为等边三角形,则SD=BD,再由E为SB的中点,得到DE⊥SB,结合已知利用线面垂直的判定得,DE⊥平面SBC,再由面面垂直的判断得答案;
(3)在图中作出二面角B-SC-D的平面角,然后通过解三角形求得边长,再解直角三角形求得二面角B-SC-D的正弦值.
解答 (1)证明:如图,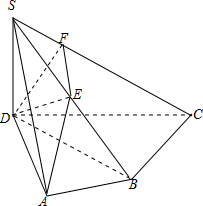 ∵SD⊥平面ABCD,BC?平面ABCD,∴BC⊥SD,
∵SD⊥平面ABCD,BC?平面ABCD,∴BC⊥SD,
又∵BC⊥BD,SD∩BD=D,∴BC⊥面SBD,
∵DE?面SBD,∴BC⊥DE;
(2)证明:∵SD=AD=AB,∠ABD=60°,∴△ABD为等边三角形,则SD=BD,
又E为SB的中点,∴DE⊥SB,
又∵BC⊥DE,SB∩BC=B,∴DE⊥平面SBC,
又DE?平面SBD,∴平面SBC⊥平面ADE;
(3)解:过E作EF⊥SC于F,连DF,∴DF⊥SC,则∠DEF为二面角B-SC-D的平面角;
在Rt△SDB中,设SD=a,由(2)中证得的SD=BD,可得BD=a,
∴$SB=\sqrt{S{D}^{2}+B{D}^{2}}=\sqrt{{a}^{2}+{a}^{2}}=\sqrt{2}a$,
∴$DE=\frac{{\sqrt{2}}}{2}a,\frac{DB}{DC}=cos{30°},DC=\frac{DB}{{cos{{30}°}}}=\frac{{2\sqrt{3}}}{3}a$,
∴$DF×SC=SD×DC,SC=\sqrt{{a^2}+\frac{12}{9}{a^2}}=\frac{{\sqrt{21}}}{3}a$,
∴$DF=\frac{{a×\frac{{2\sqrt{3}}}{3}a}}{{\frac{{\sqrt{21}}}{3}a}}=\frac{{2\sqrt{7}}}{7}a$,
则$sin∠EDF=\frac{DE}{DF}=\frac{{\sqrt{2}}}{2}a×\frac{7}{{2\sqrt{7}a}}=\frac{{\sqrt{14}}}{4}$.
∴二面角B-SC-D的正弦值为$\frac{{\sqrt{14}}}{4}$.
点评 本题主要考查直线与平面之间的平行、垂直等位置关系,二面角的概念、求法等知识,以及空间想象能力和逻辑推理能力,是中档题.

| A. | an=$\frac{n-1}{2}$ | B. | an=n-1 | C. | an=(n-1)2 | D. | an=2n-2 |
| A. | ($\frac{5}{13}$,-$\frac{12}{13}$) | B. | (-$\frac{5}{13}$,$\frac{12}{13}$) | C. | ($\frac{12}{13}$,-$\frac{5}{13}$) | D. | (-$\frac{12}{13}$,$\frac{5}{13}$) |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |