题目内容
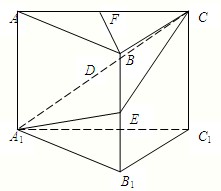
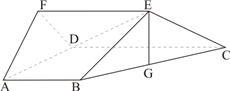
设多面体ABCDEF,已知AB∥CD∥EF,平面ABCD⊥平面ADF,△ADF是以AD为斜边的等腰直角三角形,若∠ADC=120°,AD=2,AB=2,CD=4,EF=3,G为BC的中点.
(1)求证:EG∥平面ADF;
(2)求直线DE与平面ABCD所成角的余弦值.
(1)求证:EG∥平面ADF;
(2)求直线DE与平面ABCD所成角的余弦值.

(1)证明:如图,设H是AD的中点,可得GH=3,则GH=EF,
又∵GH∥CD,EF∥CD
∴GH∥EF,则EFHG为平行四边形,
故EG∥FH,
又∵FH?平面ADF
∴EG∥平面ADF;
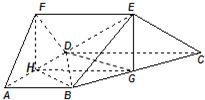
(2)∵△ADF是以AD为斜边的等腰直角三角形.
∴FH⊥AD,
又∵平面ADF⊥平面ABCD
∴FH⊥平面ABCD,
∴EG⊥平面ABCD
∴∠EDG是直线DE与平面ABCD所成的角
∵∠ADC=120°,∴∠BAD=60°,
又∵AB=AD=2,∴BD=2∴∠ADB=60°,
又∵CD=4,由余弦定理BC=2
∴∠DBC=90°,BG=
,
∴DG=
又∵EG=FH=1,∴DE=2
,
∴cos∠EDG=
=
所以直线DE与平面ABCD所成角的余弦值
.
又∵GH∥CD,EF∥CD
∴GH∥EF,则EFHG为平行四边形,
故EG∥FH,
又∵FH?平面ADF
∴EG∥平面ADF;
(2)∵△ADF是以AD为斜边的等腰直角三角形.
∴FH⊥AD,
又∵平面ADF⊥平面ABCD
∴FH⊥平面ABCD,
∴EG⊥平面ABCD
∴∠EDG是直线DE与平面ABCD所成的角
∵∠ADC=120°,∴∠BAD=60°,
又∵AB=AD=2,∴BD=2∴∠ADB=60°,
又∵CD=4,由余弦定理BC=2
| 3 |
∴∠DBC=90°,BG=
| 3 |
∴DG=
| 7 |
又∵EG=FH=1,∴DE=2
| 2 |
∴cos∠EDG=
| DG |
| DE |
| ||
| 4 |
所以直线DE与平面ABCD所成角的余弦值
| ||
| 4 |


练习册系列答案
相关题目