题目内容
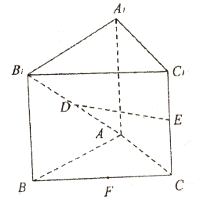
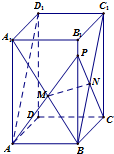
在长方体ABCD-A1B1C1D1中，AD=
，AA1=2，如图，
（1）当点P在BB1上运动时（点P∈BB1，且异于B，B1）设PA∩BA1=M，PC∩BC1=N，求证：MN∥平面ABCD
（2）当点P是BB1的中点时，求异面直线PC与AD1所成角的正弦值．
| 2 |
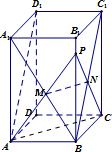
（1）当点P在BB1上运动时（点P∈BB1，且异于B，B1）设PA∩BA1=M，PC∩BC1=N，求证：MN∥平面ABCD
（2）当点P是BB1的中点时，求异面直线PC与AD1所成角的正弦值．
（1）证明：连接MN，∵BP∥AA1，∴
=
，
同理
=
，∵AA1=CC1，∴
=
，∴MN∥AC，
又AC?平面ABCD，MN?平面ABCD，∴MN∥平面ABCD．
（2）∵AB∥C1D1，AB=C1D1，∴四边形ABC1D1为平行四边形，
∴AD1∥BC1，∴∠BNC为异面直线PC与AD1所成角，
∵点P是BB1的中点，∴BP=1=
CC1，∴BN=
NC1=
AC1=
，
CN=2PN=
PC=
，BC=
，
由余弦定理得cos∠BNC=
=0，
∴sin∠BNC=1．
| PM |
| MA |
| BP |
| AA1 |
同理
| PN |
| NC |
| BP |
| CC1 |
| PM |
| MA |
| PN |
| NC |
又AC?平面ABCD，MN?平面ABCD，∴MN∥平面ABCD．
（2）∵AB∥C1D1，AB=C1D1，∴四边形ABC1D1为平行四边形，
∴AD1∥BC1，∴∠BNC为异面直线PC与AD1所成角，
∵点P是BB1的中点，∴BP=1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| ||
| 3 |
CN=2PN=
| 2 |
| 3 |
2
| ||
| 3 |
| 2 |
由余弦定理得cos∠BNC=
| BN2+CN2-BC2 |
| 2×BN×CN |
∴sin∠BNC=1．
练习册系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
