题目内容
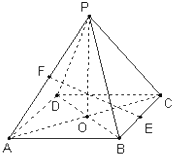
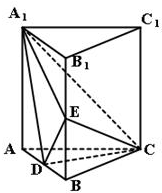
如图,已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,P为AD1的中点,(1)求证:直线C1P∥平面AB1C;(2)求异面直线AA1与B1P所成角的余弦值.
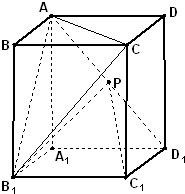

(1)证明:取B1C中点Q,连接AQ,QC1,
则QC1∥AP且QC1=AP,所以四边形APC1Q是平行四边形,所以PC1∥AQ,
又AQ?平面AB1C,C1P?平面AB1C,所以直线C1P∥平面AB1C
(2)解法一:过点P作PE⊥A1D1,垂足为E,连接B1E(如图),
则PE∥AA1,∴∠B1PE是异面直线AA1与B1P所成的角.
在 Rt△AA1D1中∵∠AD1A1=60°
∴∠A1AD1=30°
∴A1B1=A1D1=
AD1=2,A1E=
A1D1=1,
∴B1E=
=
.
又PE=
AA1=
.
∴在 Rt△B1PE中,B1P=
=2
cos∠B1PE=
=
=
.
∴异面异面直线AA1与B1P所成角的余弦值为
.
 解法二:以A1为原点,A1B1所在的直线为x轴建立空间直角坐标系如图示,
解法二:以A1为原点,A1B1所在的直线为x轴建立空间直角坐标系如图示,
则A1(0,0,0),A(0,0,2
),B1(2,0,0),P(0,1,
),
∴
=(0,0,2
),
=(-2,1,
)
∴cos<
,
>=
=
=
.
∴异面异面直线AA1与B1P所成角的余弦值为
.

则QC1∥AP且QC1=AP,所以四边形APC1Q是平行四边形,所以PC1∥AQ,
又AQ?平面AB1C,C1P?平面AB1C,所以直线C1P∥平面AB1C
(2)解法一:过点P作PE⊥A1D1,垂足为E,连接B1E(如图),
则PE∥AA1,∴∠B1PE是异面直线AA1与B1P所成的角.
在 Rt△AA1D1中∵∠AD1A1=60°
∴∠A1AD1=30°
∴A1B1=A1D1=
| 1 |
| 2 |
| 1 |
| 2 |
∴B1E=
| B1A12+A1E2 |
| 5 |
又PE=
| 1 |
| 2 |
| 3 |
∴在 Rt△B1PE中,B1P=
| 5+3 |
| 2 |
| PE |
| B1P |
| ||
2
|
| ||
| 4 |
∴异面异面直线AA1与B1P所成角的余弦值为
| ||
| 4 |
 解法二:以A1为原点,A1B1所在的直线为x轴建立空间直角坐标系如图示,
解法二:以A1为原点,A1B1所在的直线为x轴建立空间直角坐标系如图示,则A1(0,0,0),A(0,0,2
| 3 |
| 3 |
∴
| A1A |
| 3 |
| B1P |
| 3 |
∴cos<
| A1A |
| B1P |
| ||||
|
|
| 6 | ||||
2
|
| ||
| 4 |
∴异面异面直线AA1与B1P所成角的余弦值为
| ||
| 4 |


练习册系列答案
相关题目