题目内容
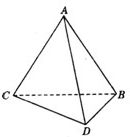
已知四面体ABCD，AD=CD，∠ADB=∠CDB=120°，且平面ABD⊥平面BCD．
（Ⅰ）求证：BD⊥AC；
（Ⅱ）求直线CA与平面ABD所成角的大小．
（Ⅰ）求证：BD⊥AC；
（Ⅱ）求直线CA与平面ABD所成角的大小．
（Ⅰ）证明：∵AD=DC，∠ADB=∠CDB=120°，BD=BD
∴△ADB≌△CDB
∴AB=BC，取AC中点M，
则MB⊥AC，DM⊥AC
∴AC⊥平面BDM，
∴AC⊥BD．
（Ⅱ）过点C作CH⊥BD交BD延长线于H，连结HA，
∵平面ABD⊥平面BCD，∴CH⊥平面BAD，
∴∠CAH为CA与平面BAD所成角，
∵DC=AD，∠ADH=∠CDH=60°，DH=DH，
∴△HAD≌△CDHk，
∴AH=HC
∴在Rt△HAC中，∠HAC=45°
∴直线CA与平面ABD所成角的大小为45°．
∴△ADB≌△CDB
∴AB=BC，取AC中点M，则MB⊥AC，DM⊥AC
∴AC⊥平面BDM，
∴AC⊥BD．
（Ⅱ）过点C作CH⊥BD交BD延长线于H，连结HA，
∵平面ABD⊥平面BCD，∴CH⊥平面BAD，
∴∠CAH为CA与平面BAD所成角，
∵DC=AD，∠ADH=∠CDH=60°，DH=DH，∴△HAD≌△CDHk，
∴AH=HC
∴在Rt△HAC中，∠HAC=45°
∴直线CA与平面ABD所成角的大小为45°．
练习册系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
