题目内容
已知a和b是成60°角的两条异面直线，则过空间一点且与a和b都成60°角的直线共有（ ）
| A．1条 | B．2条 | C．3条 | D．4条 |
把异面直线a，b平移到相交，使交点为P，
此时∠APB=60°，过P点作直线a，b相交所成角的两条角平分线c，d，如图所示：
若存在其它直线与a，b都成60°角，则直线在该平面上的射影为c或d
∵d与a，b都成60°角，则在平面上射影为d的直线只有直线d一条，
∵c与a，b都成30°角，由三余弦定理，当直线与c夹角的余弦为
时，满足条件，这样的直线共有2条，
故过空间一点且与a和b都成60°角的直线共有3条
故选C
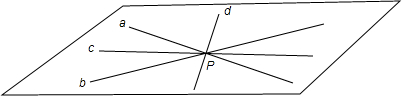
此时∠APB=60°，过P点作直线a，b相交所成角的两条角平分线c，d，如图所示：
若存在其它直线与a，b都成60°角，则直线在该平面上的射影为c或d
∵d与a，b都成60°角，则在平面上射影为d的直线只有直线d一条，
∵c与a，b都成30°角，由三余弦定理，当直线与c夹角的余弦为
| ||
| 3 |
故过空间一点且与a和b都成60°角的直线共有3条
故选C
练习册系列答案
考前必练系列答案
相关题目
