题目内容
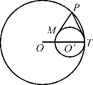
如图,圆O与圆O′内切于点T,点P为外圆O上任意一点,PM与内圆O′切于点M.求证:PM∶PT为定值.

见解析
证明:设外圆半径为R,内圆半径为r,作两圆的公切线TQ.
设PT交内圆于C,连结OP,O′C,则PM2=PC·PT,所以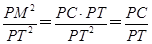 .
.
由弦切角定理知∠POT=2∠PTQ,∠CO′T=2∠PTQ,
则∠POT=∠CO′T,所以PO∥CO′,
所以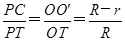 ,即
,即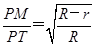 ,为定值.
,为定值.
设PT交内圆于C,连结OP,O′C,则PM2=PC·PT,所以
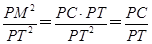 .
.由弦切角定理知∠POT=2∠PTQ,∠CO′T=2∠PTQ,
则∠POT=∠CO′T,所以PO∥CO′,
所以
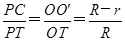 ,即
,即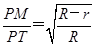 ,为定值.
,为定值.
练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
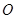 的两弦
的两弦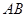 和
和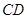 交于点
交于点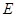 ,
,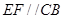 ,
,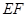 交
交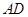 的延长线于点
的延长线于点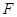 .求证:△
.求证:△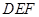 ∽△
∽△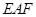 .
.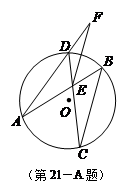

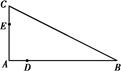
 ,则线段CD的长为________.
,则线段CD的长为________.
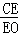 的值为 _________ .
的值为 _________ .
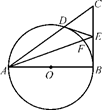
 的直径
的直径 ,
, 为
为 ,过点
,过点 的
的 延长线于点
延长线于点 ,则
,则 ________;
________;
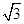 ,求圆O的半径长和∠EFD的大小.
,求圆O的半径长和∠EFD的大小.