题目内容
(本题满分12分)
已知函数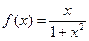 .
.
(Ⅰ)判断函数 的奇偶性;
的奇偶性;
(Ⅱ)指出该函数在区间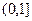 上的单调性,并用单调性定义证明;
上的单调性,并用单调性定义证明;
(Ⅲ)对于任意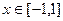 ,
, 恒成立,求实数
恒成立,求实数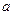 的取值范围.
的取值范围.
已知函数
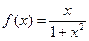 .
.(Ⅰ)判断函数
 的奇偶性;
的奇偶性;(Ⅱ)指出该函数在区间
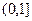 上的单调性,并用单调性定义证明;
上的单调性,并用单调性定义证明;(Ⅲ)对于任意
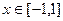 ,
, 恒成立,求实数
恒成立,求实数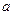 的取值范围.
的取值范围.(Ⅰ) 是奇函数.
是奇函数.
(Ⅱ) 在
在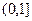 上是增函数;证明略
上是增函数;证明略
(Ⅲ)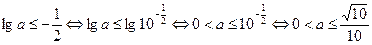
 是奇函数.
是奇函数.(Ⅱ)
 在
在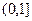 上是增函数;证明略
上是增函数;证明略(Ⅲ)
解:(Ⅰ)函数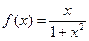 的定义域为
的定义域为 ,┈┈ 1分
,┈┈ 1分
 ┈┈ 1分
┈┈ 1分
 是奇函数. ┈┈ 1分
是奇函数. ┈┈ 1分
(Ⅱ)函数 在区间
在区间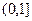 上是增函数;┈┈ 1分
上是增函数;┈┈ 1分
用单调性定义证明如下:设 ,则
,则
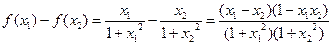 ┈┈ 1分
┈┈ 1分
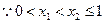 ,
, ,且
,且
┈┈ 1分
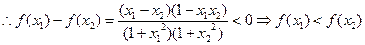 ,┈┈ 1分
,┈┈ 1分
即 在
在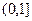 上是增函数;┈┈ 1分
上是增函数;┈┈ 1分
(Ⅲ)由(Ⅰ)(Ⅱ)知当 时,
时,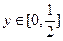 ;┈┈ 1分
;┈┈ 1分
又 是奇函数,根据对称性得,当
是奇函数,根据对称性得,当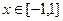 时,
时, ;┈┈ 1分
;┈┈ 1分
 对于任意
对于任意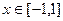 ,
, 恒成立
恒成立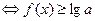 恒成立,
恒成立,

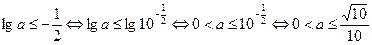 .┈┈ 2分
.┈┈ 2分
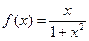 的定义域为
的定义域为 ,┈┈ 1分
,┈┈ 1分 ┈┈ 1分
┈┈ 1分 是奇函数. ┈┈ 1分
是奇函数. ┈┈ 1分(Ⅱ)函数
 在区间
在区间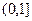 上是增函数;┈┈ 1分
上是增函数;┈┈ 1分用单调性定义证明如下:设
 ,则
,则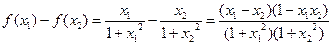 ┈┈ 1分
┈┈ 1分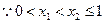 ,
, ,且
,且
┈┈ 1分
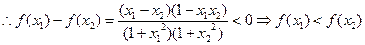 ,┈┈ 1分
,┈┈ 1分即
 在
在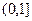 上是增函数;┈┈ 1分
上是增函数;┈┈ 1分(Ⅲ)由(Ⅰ)(Ⅱ)知当
 时,
时,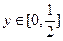 ;┈┈ 1分
;┈┈ 1分又
 是奇函数,根据对称性得,当
是奇函数,根据对称性得,当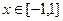 时,
时, ;┈┈ 1分
;┈┈ 1分 对于任意
对于任意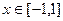 ,
, 恒成立
恒成立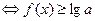 恒成立,
恒成立,
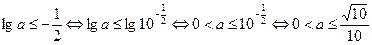 .┈┈ 2分
.┈┈ 2分
练习册系列答案
相关题目
 年利润为
年利润为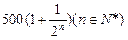 万元。
万元。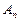 万元;若进行技术改造后,则从2006年起的前
万元;若进行技术改造后,则从2006年起的前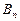 万元,分别求
万元,分别求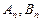 ;
;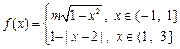 ,其中m > 0,若方程
,其中m > 0,若方程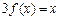 恰有5个实数解,则m的取值范围为( )
恰有5个实数解,则m的取值范围为( )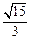 ,
, )
) )
) ,
,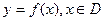 ,那么集合
,那么集合 中所含元素的个数是 ( )
中所含元素的个数是 ( )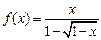 的定义域是。
的定义域是。  ( )
( ) 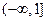
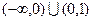
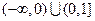

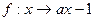 为从集合A到B的映射,若
为从集合A到B的映射,若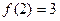 ,则
,则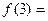 _____________.
_____________. 相等的左中右三个矩形栏目,这三栏的面积之和为60 000
相等的左中右三个矩形栏目,这三栏的面积之和为60 000  ,四周空白的宽度为10 cm,栏与栏之间的中缝空白的宽度为5 cm,怎样确定广告矩形栏目高与宽的尺寸(单位:cm),能使整个矩形广告面积最小.
,四周空白的宽度为10 cm,栏与栏之间的中缝空白的宽度为5 cm,怎样确定广告矩形栏目高与宽的尺寸(单位:cm),能使整个矩形广告面积最小.