Question

【题目】在平面直角坐标系中，抛物线C：（）的焦点为

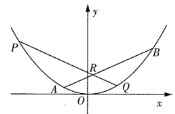
（1）动直线l过F点且与抛物线C交于M，N两点，点M在y轴的左侧，过点M作抛物线C准线的垂线，垂足为M1，点E在上，且满足连接并延长交y轴于点D，的面积为，求抛物线C的方程及D点的纵坐标；

（2）点H为抛物线C准线上任一点，过H作抛物线C的两条切线,，切点为A，B，证明直线过定点，并求面积的最小值.

Answer 1

【答案】（1）；（0，4）（2）证明见解析，面积最小值为4

【解析】

(1)由焦点坐标，可得抛物线的方程,设，由向量共线定理可得,求得M的坐标，代入抛物线方程可得，即可求解；

（2））设点，，，根据导数的几何意义，求得抛物线在A, B处的切线的方程，由两点确定一直线可得AB的方程，进而得到恒过定点F,再讨论t=0, ，写出即可求最值.

（1）因为，所以抛物线C：，

设，

因为，，，

所以，，

又因为，，推出，

M在抛物线C上，，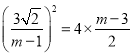

解得，故 D（0,4）

（2）设点，，.

由C：，

即，得，

所以抛物线C：在点处的切线的方程为，

即，

因为，，

因为在切线上，

所以①

同理②；

综合①②得，点，的坐标满足方程，

即直线恒过抛物线焦点.

当时，此时，可知，

当时，此时直线的斜率为，得，

于是，而，

把直线代入C：中，消去x得，，

即，

当时，最小，且最小值为4.