Question

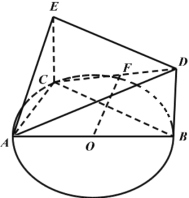
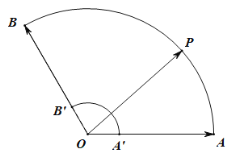
【题目】已知扇环如图所示，是扇环边界上一动点，且满足，则的取值范围为_________.

Answer 1

【答案】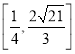

【解析】

建立直角坐标系，易知，分以下四种情况讨论：（1）当点在上运动时；（2）当点在上运动时；（3）当点在上运动时；（4）当点在上运动时.（1）（2）根据点P的坐标范围可得出x和y的范围，从而可求的范围；（3）（4）同理，可利用圆的的参数方程表示，从而得到的三角函数表达式，根据辅助角公式即可得到结果.

以为坐标原点，以为轴建立平面直角坐标系，易知，

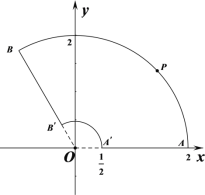
（1）当点在上运动时，向量与共线，显然，

此时，因为点在上，

其横坐标满足：，所以；

（2）当点在上运动时，向量与共线，显然，

此时，因为点在上，

其横坐标满足：，

则，所以；

（3）当点在上运动时，设，

由，得，

即，可得，

变形可得，其中，

因为是扇环边界上一动点，且满足，所以均为非负实数，

，因为，

所以当时，取得最大值，的最大值为，

由，所以当时，取得最大角，

此时取得最小值，即，

所以，的最小值为1；

（4）同理可得当点在上运动时，因为，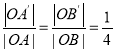

故的最大值为，最小值为.

综上所述，.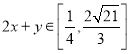

【点晴】

本题考查平面向量的综合应用，解题的关键是三角恒等变形、分类讨论思想以及数形结合的应用，属难题.