Question

【题目】已知，是双曲线的左、右焦点，点P为上异于顶点的点，直线l分别与以，为直径的圆相切于A，B两点，若向量，的夹角为，则=___________.

Answer 1

【答案】

【解析】

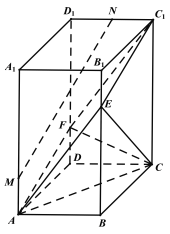
首先将图象画出来，设以PF1，PF2为直径的圆的圆心分别为C，D，连接AC，BD，过D作DE⊥AC于点E，连接CD，易证四边形ABDE是矩形，根据几何关系可得|CE|===5，由可得，又向量的夹角即为的夹角，从而.

如图，设以PF1，PF2为直径的圆的圆心分别为C，D，连接AC，BD，

过D作DE⊥AC于点E，连接CD，则，

因为直线AB是圆C和圆D的公切线，且切点分别是A，B，

所以AC⊥AB，BD⊥AB，则四边形ABDE是矩形，所以|AB|=|DE|，|AE|=|BD|.

且，，易知|CE|=|AC|-|AE|=|AC|-|BD|=，

根据双曲线的定义知，|PF1|-|PF2|=10，所以|CE|=5.

因为，由|可得，

即|AB|=3，因为向量的夹角即为的夹角，

所以.

故答案为：.