题目内容
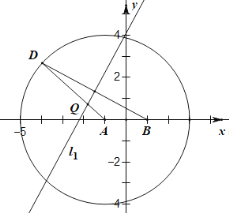
【题目】在平面直角坐标系xOy中,椭圆![]() 的左、右顶点分别为A、B,右焦点为F,且点F满足
的左、右顶点分别为A、B,右焦点为F,且点F满足![]() ,由椭圆C的四个顶点围成的四边形面积为
,由椭圆C的四个顶点围成的四边形面积为![]() .过点
.过点![]() 的直线TA,TB与此椭圆分别交于点
的直线TA,TB与此椭圆分别交于点![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() .
.
(1)求椭圆C的标准方程;
(2)当T在直线![]() 时,直线MN是否过x轴上的一定点?若是,求出该定点的坐标;若不是,请说明理由.
时,直线MN是否过x轴上的一定点?若是,求出该定点的坐标;若不是,请说明理由.
【答案】(1)![]() (2)直线MN必过x轴上一定点
(2)直线MN必过x轴上一定点![]() .
.
【解析】
(1)根据题意求出![]() 的值,得到椭圆方程.
的值,得到椭圆方程.
(2)计算![]() 和
和![]() 的直线方程,联立方程计算
的直线方程,联立方程计算![]() 坐标,讨论
坐标,讨论![]() 和
和![]() 两种情况,计算得到答案.
两种情况,计算得到答案.
(1)由![]() 知
知![]() ,
,![]() ,
,
由椭圆C的四个顶点围成的四边形面积为![]() ,
,
又有![]() ,解得
,解得![]() ,
,![]() ,所以椭圆C的标准方程为
,所以椭圆C的标准方程为![]() .
.
(2)可知![]() ,直线AT的方程为
,直线AT的方程为![]() ,直线BT的方程为
,直线BT的方程为![]() .
.
点![]() 满足
满足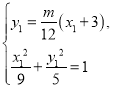
![]() ,故
,故![]() ,
,![]() .
.
点![]() 满足
满足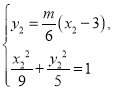
![]() ,故
,故![]() ,
,![]() .
.
若![]() ,则
,则![]() 且
且![]() ,得
,得![]() ,
,
此时直线MN的方程为![]() ,过点
,过点![]() ;
;
若![]() ,则
,则![]() ,
,
直线MD的斜率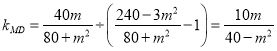 ,
,
直线MD的斜率为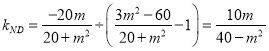 ,
,
所在![]() ,所以直线MN过点
,所以直线MN过点![]() ,
,
因此直线MN必过x轴上一定点![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目