题目内容
直三棱柱ABC-A1B1C1中, AC=BC=AA1=2,∠ACB=90°.E为BB1的中点,D点在AB上且DE=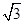 .
.
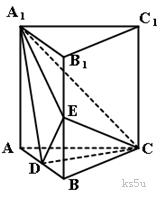
(Ⅰ)求证:CD⊥平面A1ABB1;
(Ⅱ)求三棱锥A1-CDE的体积.
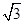 .
.
(Ⅰ)求证:CD⊥平面A1ABB1;
(Ⅱ)求三棱锥A1-CDE的体积.
(1)见解析 (2)三棱锥A1-CDE的体积为1.
(1)证明线面垂直根据判断定理,只需要证明直线垂直这个平面内的两条相交直线即可.本小题可以证明CD⊥AB, CD⊥AA1即可.
(2)本小题求面积不易直接求,采用整体减去部分的作法求解.本小题可以用 求解
求解
(1)在Rt△DBE中,BE=1,DE=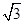 ,∴BD=
,∴BD= =
=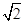 =
=  AB,
AB,
∴ 则D为AB中点, 而AC=BC, ∴CD⊥AB
又∵三棱柱ABC-A1B1C1为直三棱柱, ∴CD⊥AA1
又 AA1∩AB="A" 且 AA1、AB Ì平面A1ABB1
故 CD⊥平面A1ABB1 6分
(2)∵四边形A1ABB1为矩形,∴△A1AD,△DBE,△EB1A1都是直角三角形,
∴
=2×2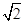 -
- ×
×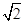 ×2-
×2- ×
×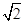 ×1-
×1- ×2
×2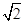 ×1=
×1= 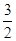
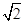
∴ VA1-CDE =VC-A1DE =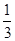 ×SA1DE ×CD=
×SA1DE ×CD= 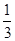 ×
×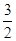
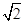 ×
×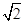 =1
=1
∴ 三棱锥A1-CDE的体积为1
(2)本小题求面积不易直接求,采用整体减去部分的作法求解.本小题可以用
 求解
求解(1)在Rt△DBE中,BE=1,DE=
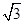 ,∴BD=
,∴BD= =
=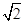 =
=  AB,
AB,∴ 则D为AB中点, 而AC=BC, ∴CD⊥AB
又∵三棱柱ABC-A1B1C1为直三棱柱, ∴CD⊥AA1
又 AA1∩AB="A" 且 AA1、AB Ì平面A1ABB1
故 CD⊥平面A1ABB1 6分
(2)∵四边形A1ABB1为矩形,∴△A1AD,△DBE,△EB1A1都是直角三角形,
∴

=2×2
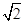 -
- ×
×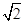 ×2-
×2- ×
×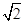 ×1-
×1- ×2
×2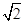 ×1=
×1= 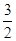
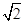
∴ VA1-CDE =VC-A1DE =
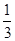 ×SA1DE ×CD=
×SA1DE ×CD= 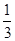 ×
×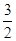
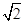 ×
×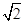 =1
=1∴ 三棱锥A1-CDE的体积为1

练习册系列答案
相关题目
 ;
; 的体积;
的体积; 

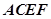 所在平面与矩形
所在平面与矩形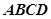 所在平面垂直,
所在平面垂直,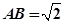 ,
,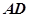 =1,
=1,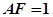 ,
,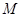 是线段
是线段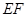 的中点.
的中点.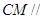 平面
平面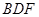 ;
;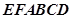 的表面积;
的表面积;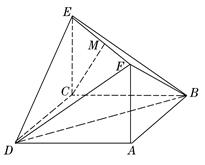

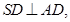 且
且 ,
,
 。(I)求多面体ABCDS的体积;(II)求AD与SB所成角的余弦值;(III)求二面角A—SB—D的余弦值。
。(I)求多面体ABCDS的体积;(II)求AD与SB所成角的余弦值;(III)求二面角A—SB—D的余弦值。
 ,OC=
,OC= ,则三棱锥O-ABC外接球的表面积为( )
,则三棱锥O-ABC外接球的表面积为( ) 的边长为2,点
的边长为2,点 、
、 分别在边
分别在边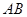 、
、 上,且
上,且 ,
, ,将此正方形沿
,将此正方形沿 、
、 折起,使点
折起,使点 、
、 重合于点
重合于点 ,则三棱锥
,则三棱锥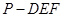 的体积是
的体积是



 ,其余棱长都为1,其体积为
,其余棱长都为1,其体积为 ,则函数
,则函数