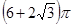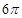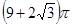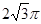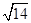题目内容
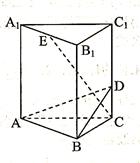
如图,多面体ABCDS中,面ABCD为矩形,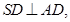 且
且 ,
,
 。(I)求多面体ABCDS的体积;(II)求AD与SB所成角的余弦值;(III)求二面角A—SB—D的余弦值。
。(I)求多面体ABCDS的体积;(II)求AD与SB所成角的余弦值;(III)求二面角A—SB—D的余弦值。
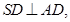 且
且 ,
,
 。(I)求多面体ABCDS的体积;(II)求AD与SB所成角的余弦值;(III)求二面角A—SB—D的余弦值。
。(I)求多面体ABCDS的体积;(II)求AD与SB所成角的余弦值;(III)求二面角A—SB—D的余弦值。
(1)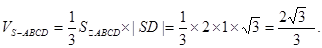 (2)
(2)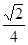 ;(3)
;(3)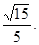
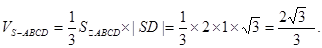 (2)
(2)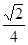 ;(3)
;(3)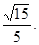
本试题主要是考查同学们运用点线面的位置关系,求解异面直线所成的角,以及二面角的求解问题。培养了同学们的空间想象能力和逻辑推理能力和计算能力的运用。
(1)因为多面体ABCDS的体积即四棱锥S—ABCD的体积。利用棱锥的体积公式求解得到。
(2)分析; 要求AD与SB所成的角,即求BC与SB所成的角,那么利用平移法得到角,解三角形得到结论。
(3)利用三垂线定理得到二面角,然后借助于三角形的知识求解得到。
解:(I)多面体ABCDS的体积即四棱锥S—ABCD的体积。
所以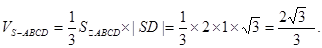
II)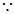 矩形ABCD,
矩形ABCD,
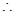 AD//BC,即BC=a,
AD//BC,即BC=a, 要求AD与SB所成的角,即求BC与SB所成的角在
要求AD与SB所成的角,即求BC与SB所成的角在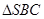 中,由(1)知
中,由(1)知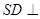 面ABCD。
面ABCD。
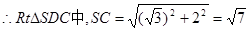
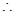 CD是CS在面ABCD内的射影,且
CD是CS在面ABCD内的射影,且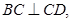
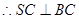
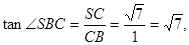
 BC与SB所成的角的余弦为
BC与SB所成的角的余弦为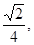
从而SB与AD的成的角的余弦为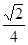
(III)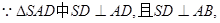
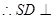 面ABCD。
面ABCD。
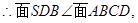 BD为面SDB与面ABCD的交线。
BD为面SDB与面ABCD的交线。
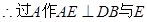
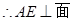 SDB
SDB
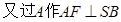 于F,连接EF从而得:
于F,连接EF从而得: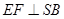
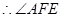 为二面角A—SB—D的平面角
为二面角A—SB—D的平面角
在矩形ABCD中,对角线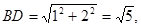
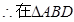 中,
中,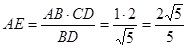
由(2)知在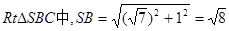
而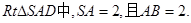
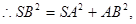
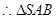 为等腰直角三角形且
为等腰直角三角形且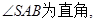
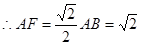
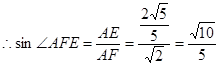 ,
,
所以所求的二面角的余弦为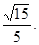
(1)因为多面体ABCDS的体积即四棱锥S—ABCD的体积。利用棱锥的体积公式求解得到。
(2)分析; 要求AD与SB所成的角,即求BC与SB所成的角,那么利用平移法得到角,解三角形得到结论。
(3)利用三垂线定理得到二面角,然后借助于三角形的知识求解得到。
解:(I)多面体ABCDS的体积即四棱锥S—ABCD的体积。
所以
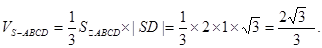
II)
 矩形ABCD,
矩形ABCD,
|
 AD//BC,即BC=a,
AD//BC,即BC=a, 要求AD与SB所成的角,即求BC与SB所成的角在
要求AD与SB所成的角,即求BC与SB所成的角在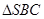 中,由(1)知
中,由(1)知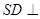 面ABCD。
面ABCD。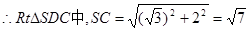
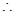 CD是CS在面ABCD内的射影,且
CD是CS在面ABCD内的射影,且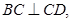
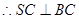
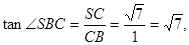
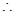 BC与SB所成的角的余弦为
BC与SB所成的角的余弦为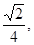
从而SB与AD的成的角的余弦为
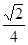
(III)
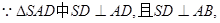
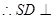 面ABCD。
面ABCD。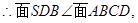 BD为面SDB与面ABCD的交线。
BD为面SDB与面ABCD的交线。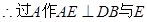
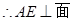 SDB
SDB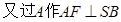 于F,连接EF从而得:
于F,连接EF从而得: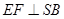
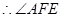 为二面角A—SB—D的平面角
为二面角A—SB—D的平面角在矩形ABCD中,对角线
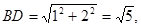
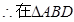 中,
中,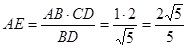
由(2)知在
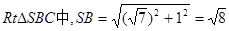
而
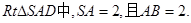
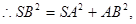
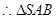 为等腰直角三角形且
为等腰直角三角形且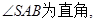
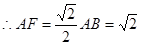
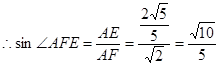 ,
,所以所求的二面角的余弦为

练习册系列答案
相关题目
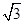 .
.
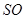 的侧面积为
的侧面积为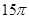 ,底面半径
,底面半径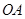 和
和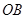 互相垂直,且
互相垂直,且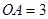 ,
,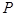 是母线
是母线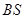 的中点.
的中点.
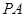 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).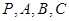 在同一球面上,且
在同一球面上,且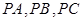 两两垂直,
两两垂直, ,那么这个球的表面积是( )
,那么这个球的表面积是( ) 



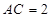 ,
,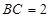 ,∠ACB=120°,若△ABC绕直线BC旋转一周,则所形成的几何体的表面积是
,∠ACB=120°,若△ABC绕直线BC旋转一周,则所形成的几何体的表面积是