题目内容
【题目】如图，在棱台ABC﹣FED中，△DEF与△ABC分别是棱长为1与2的正三角形，平面ABC⊥平面BCDE，四边形BCDE为直角梯形，BC⊥CD，CD=1，N为CE中点， 
．
（1）λ为何值时，MN∥平面ABC？
（2）在（1）的条件下，求直线AN与平面BMN所成角的正弦值． 
【答案】
（1）解：当 
，即M为AF中点时MN∥平面ABC．
事实上，取CD中点P，连接PM，PN，
∵AM=MF，CP=PD，∴MP∥AC，
∵AC平面ABC，MP平面ABC，∴MP∥平面ABC．
由CP∥PD，CN∥NE，得NP∥DE，
又DE∥BC，∴NP∥BC，
∵BC平面ABC，NP平面ABC，∴NP∥平面ABC．
∴平面MNP∥平面ABC，则MN∥平面ABC；
（2）解：取BC中点O，连OA，OE，
∵AB=AC，OB=OC，∴AO⊥BC，
∵平面ABC⊥平面BCDE，且AO平面ABC，∴AO⊥平面BCDE，
∵OC= 
，BC∥ED，∴OE∥CD，
又CD⊥BC，∴OE⊥BC．
分别以OE，OC，OA所在直线为x轴，y轴，z轴，建立空间直角坐标系．
则A（0，0， 
），C（0，1，0），E（1，0，0），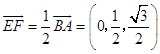 
，
∴F（1， 
， 
），M（ ， 
， 
），N（ 
）．
设 
为平面BMN的法向量，则
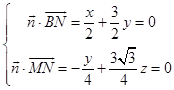，取z=1，得 
．
cos＜ 
＞= 
．
∴直线AN与平面MNB所成角的正弦值为 
．
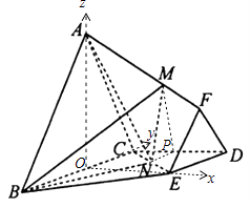
【解析】（1）取CD中点P，连接PM，PN，可得MP∥AC，则MP∥平面ABC．再由已知证明NP∥平面ABC．得到平面MNP∥平面ABC，则MN∥平面ABC；（2）取BC中点O，连OA，OE，可证AO⊥BC，OE⊥BC．分别以OE，OC，OA所在直线为x轴，y轴，z轴，建立空间直角坐标系．求出所用点的坐标，得到平面BMN的法向量，求出＜ 
＞的余弦值，即可得到直线AN与平面MNB所成角的正弦值．
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行，以及对空间角的异面直线所成的角的理解，了解已知
为两异面直线，A，C与B，D分别是上的任意两点，所成的角为
，则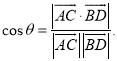
．
