题目内容
【题目】如图,四棱锥P﹣ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点. 
(1)求证:AE∥平面PCD;
(2)记平面PAB与平面PCD的交线为l,求二面角C﹣l﹣B的余弦值.
【答案】
(1)证明:∵∠ABC=∠BAD=90°,BC=2AD,E是BC的中点,
∴AD∥CE,且AD=CE,
∴四边形ADCE是平行四边形,∴AE∥CD,
∵AE平面PCD,CD平面PCD,
∴AE∥平面PCD.
(2)解:连结DE、BD,设AE∩BD于O,连结PO,
则四边形ABED是正方形,∴AE⊥BD,
∵PD=PB=2,O是BD中点,∴PO⊥BD,
则PO= ![]() =
= ![]() =
= ![]() ,
,
又OA= ![]() ,PA=2,∴PO2+OA2=PA2,
,PA=2,∴PO2+OA2=PA2,
∴△POA是直角三角形,∴PO⊥AO,
∵BD∩AE=O,∴PO⊥平面ABCD,
以O为原点,OE为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,
则P(0,0, ![]() ),A(﹣
),A(﹣ ![]() ),B(0,
),B(0, ![]() ,0),E(
,0),E( ![]() ),D(0,﹣
),D(0,﹣ ![]() ,0),
,0),
∴ ![]() =(﹣
=(﹣ ![]() ),
), ![]() =(0,
=(0, ![]() ),
), ![]() =(0,
=(0, ![]() ),
), ![]() =(2
=(2 ![]() ,0,0),
,0,0),
设 ![]() =(x,y,z)是平面PAB的法向量,
=(x,y,z)是平面PAB的法向量,
则 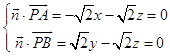 ,取x=1,得
,取x=1,得 ![]() ,
,
设 ![]() =(a,b,c)是平面PCD的法向量,
=(a,b,c)是平面PCD的法向量,
则 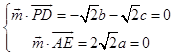 ,取b=1,得
,取b=1,得 ![]() =(0,1,﹣1),
=(0,1,﹣1),
cos< ![]() >=
>= ![]() =0,
=0,
∴二面角C﹣l﹣B的余弦值为0.

【解析】(1)推导出四边形ADCE是平行四边形,从而AE∥CD,由此能证明AE∥平面PCD.(2)连结DE、BD,设AE∩BD于O,连结PO,推导出AE⊥BD,PO⊥BD,PO⊥AO,从而PO⊥平面ABCD,以O为原点,OE为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,利用向量法能求出二面角C﹣l﹣B的余弦值.
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.

 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案【题目】某汽车的使用年数x与所支出的维修费用y的统计数据如表:
使用年数x(单位:年) | 1 | 2 | 3 | 4 | 5 |
维修总费用y(单位:万元) | 0.5 | 1.2 | 2.2 | 3.3 | 4.5 |
根据上表可得y关于x的线性回归方程 ![]() =
= ![]() x﹣0.69,若该汽车维修总费用超过10万元就不再维修,直接报废,据此模型预测该汽车最多可使用( )
x﹣0.69,若该汽车维修总费用超过10万元就不再维修,直接报废,据此模型预测该汽车最多可使用( )
A.8年
B.9年
C.10年
D.11年



